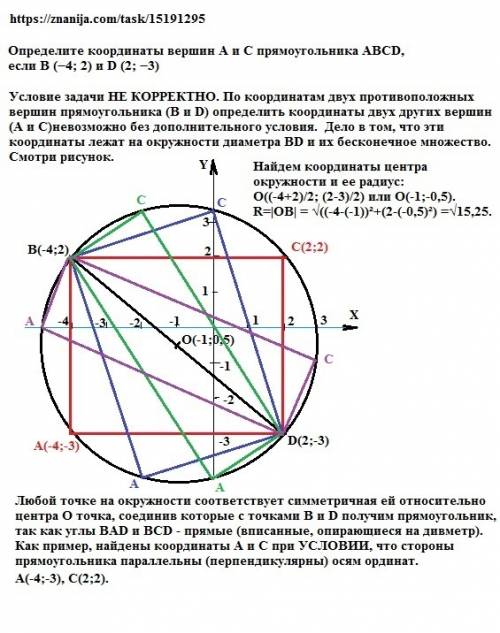
Условие задачи НЕ КОРРЕКТНО. По координатам двух противоположных вершин прямоугольника (B и D) определить координаты двух других вершин (А и С) невозможно без дополнительного условия. Дело в том, что вершины прямоугольника лежат на окружности диаметра BD и их бесконечное множество.
Смотри рисунок.
Любой точке на окружности соответствует симметричная ей относительно центра О точка, соединив которые с точками В и D получим прямоугольник, так как углы ВАD и ВСD - прямые (вписанные, опирающиеся на дивметр).
Найдем координаты центра окружности, описанной около данного прямоугольника и ее радиус:
О((-4+2)/2; (2-3)/2) или О(-1;-0,5).
R=|ОВ| = √((-4-(-1))²+(2-(-0,5)²) =√15,25. Тогда уравнение окружности (x+1)² + (y+0,5)² =15,25.
ЛЮБАЯ точка на этой окружности - вершина А, симметричная ей относительно центра О точка - вершина С.
Найдем координаты вершин А и С ПРИ УСЛОВИИ, что стороны прямоугольника параллельны осям ординат.
В уравнение окружности подставим координату Х=-4 и найдем для нее соответствующую координату Y: (-3)² + (y+0,5)² =15,25. => Y² + Y -6 = 0. => Y1=3, Y2=-2. Точно так же для точек с координатой Х=2. Y1=2 и Y2=-3. Тогда имеем: А(-4;-3) и С(2;2).
ладно, хоть я и на коленках делал, а все равно - попробую оформить.
x^2/96 + y^2 + z^2 = 1; (1/96)*x*dx + y*dy + z*dz = 0;
ищем такую точку (x0,y0,z0), принадлежащую эллипсоиду, что плоскость, определяемая уравнением
(1/96)*x0*(x - x0) + y0*(y - y0) + z0*(z - z0) = 0; (просто заменили dx = x - x0, получили касательную плоскость в точке (x0,y0,z0), это все в точности, как в одномерном случае связь производной и касательной к графику)
Самая близкая точка эллипсоида к плоскости 3x+4y+12z=288; будет там, где касательная плоскость параллельна ей. Отсюда получаем
(x0/96, y0, z0) = (3*a, 4*a, 12*a); то есть (x0,y0,z0) = (288*a,4*a,12*a);
а находится из уравнения эллипсоида.
a^2 = 1/(288^2/96 + 4^2 + 12^2) = 1/1024; a = 1/32; (минус тоже подходит, но интуитивно понятно, то решение с "плюсом" ближе к плоскости)
Мы получили точку эллипсоида, самую близкую к плоскости.
Это точка r0 = (9,1/8,3/8) (жирным выделены вектора, под r понимается радиус-вектор точки, то есть вектор из начала координат в точку (x,y,z))
Уравнение плоскости можно переписать в виде nr = 288/IаI,
где a = (3,4,12); IaI = корень(3^2 + 4^2 + 12^2) = 13; n = a/IaI - единичный вектор.
n = (3/13, 4/13, 12/13); nr = 288/13 - уравнение заданной плоскости.
Вычислим nr0 = (3*9+4*1/8+12*3/8)/13 = 32/13. Это и есть уравнение касательной плоскости в точке r0.
Поскольку скалярные произведения не зависят от выбора направления осей и расстояния - тоже, повернем оси так, чтобы n стал единичным вектором оси z.
тогда уравнения этих двух плоскостей превратятся в z = 288/13 и z = 32/13. ясно, что расстояние между ними равно 288/13 - 32/13 = 256/13.