Движение - это преобразование фигуры, которое сохраняет расстояние между ее точками.
Свойства движения:
1. Три точки, лежащие (нележащие) на одной прямой, при движении переходят в три точки, лежащие (нележащие) на одной прямой.
2. При движении прямая переходит в прямую - луч - в луч.
3. Отрезок движением переводится в отрезок.
4. Движение соханяет меры углов.
5. Последовательное выполнение двух движений есть движение.
Доказательство свойства 3. Как известно, отрезок - это часть прямой, ограниченная двумя точками. Т.к. по свойству 2 прямая переходит в прямую, то прямая, содержащая отрезок, переходит в прямую, содержащую, отрезок. А так движение сохраняет расстояние, от отрезок одной прямой переходит в равный ему отрезок другой прямой.
1).
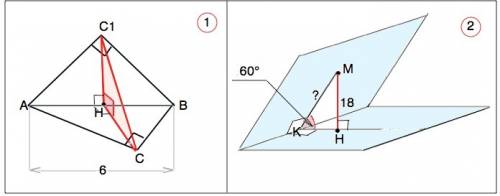
Перпендикулярные плоскости образуют двугранный угол, линейный угол которого образован лучами с общим началом на ребре двугранного угла, проведенными в его гранях перпендикулярно ребру.
Здесь грани - плоскости треугольников АВС и АВС1, ребро двугранного угла – АВ.
НС⊥АВ; НС1⊥АВ, угол СНС1=90° по условию.
∆ АВС и ∆ АВС1 равнобедренные прямоугольные, углы при их общем основании АВ равны 45°, ⇒ они равны по 2-признаку равенства треугольников.
∆ СНС1- прямоугольный. Его катеты равны высотам=медианам равных треугольников. Следовательно, он равнобедренный.
Медиана прямоугольного треугольника равна половине гипотенузы. ⇒
НС=НС1=3
СС1=3•sin45°=3√2 см
2)
Расстояние от точки М до плоскости - длина отрезка МН, проведенного между ними перпендикулярно. МН=18
Расстояние от точки М до ребра двугранного угла - длина отрезка МК, проведенного между ними перпендикулярно.
∆ МКН - прямоугольный. Его гипотенуза МК=МН:sin60°
MK=18:(√3/2)=12√3
Відповідь:
А. торфово-болотні