ответ: BC = 9 см.
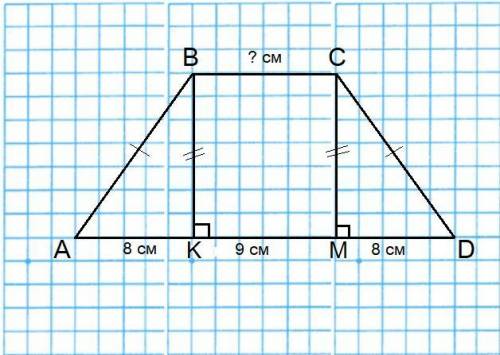
Объяснение: Обозначим равнобедренную трапецию буквами ABCD. Тогда CM - высота, которая делит основание AD на указанные отрезки.
AB и CD - боковые стороны (между собой равные по свойству).
AD - большее основание, BC - меньшее основание.
Проведём из вершины B к большему основанию трапеции AD вторую высоту BK.
BK ⊥ AD; CM ⊥ AD ⇒ BK ║ CM ⇒ BK=CM (т.е. KBCM - прямоугольник).
Рассмотрим прямоугольные ΔABK и ΔMCD. Они равны (их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что трапеция ABCD - равнобедренная).
⇒ AK = MD = 8 см.
AD = AK + KM + MD = 25 см ⇒ KM = AD - (AK + MD) = 25 - 16 = 9 см.
Т.к. KBCM - прямоугольник ⇒ KM = BC = 9 см.
AB=CB =x ; BC=AD =7x ;AB₁ =BA₁ =CD₁=DC₁=13 см ;AD₁ =DA₁ =BC₁=CB₁ =37 см.
обозн._ высота параллелепипеда AA₁ =BB₁ =CC₁ =DD₁ =h.
Sбок - ?
S бок =2(AB+BC)*AA₁ = 2(x+7x)*h =16xh.
По теореме Пифагора для треугольников ABB₁ и ADD₁:
{ AB²+BB₁² =AB₁² ; AD² +DD₁²=AD₁².
{ x²+h² =13² ; (7x)² +h²=37².
Вычитаем из второго уравнения системы первое
(7x)² -x² =37² -13²;
48x² =(37-13)(37+13) ;
2*24x² =24*2*25⇒x =5 ;
h =√(13² -5²) =12.
S бок =16xh =16*5*12 =16*60 =960 (см²).
ответ: 960 см².