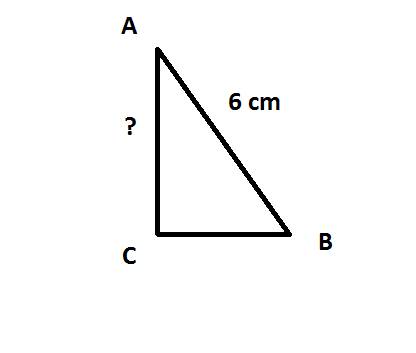
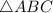 . Из условия ясно, что он — прямоугольный (так как
. Из условия ясно, что он — прямоугольный (так как 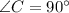 ).
). 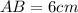 — гипотенуза,
— гипотенуза, 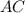 — искомый катет,
— искомый катет, 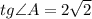
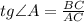
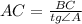
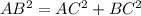
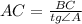 .
.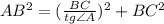
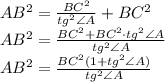
 :
: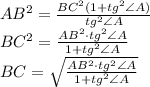
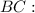
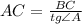
 новую подстановку:
новую подстановку: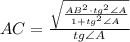
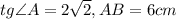
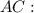
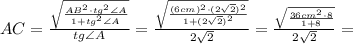
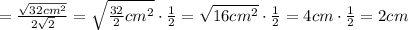

а) 60°. б) 90°.
Объяснение:
Многогранник АВСDA1B1C1D1 - параллелепипед, так как боковые ребра взаимно параллельны (дано).
а). В прямоугольнике АВСD диагонали равны и точкой пересечения делятся пополам. Следовательно, треугольник АОВ равносторонний и углы при основании равны 60°. => ∠ВАО = 60°.
Прямые А1В1 и АС - скрещивающиеся по определению: "Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными".
Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
Так как АВ параллельна А1В1, то угол между скрещивающимися прямыми А1В1 и АС равен углу между пересекающимися прямыми АВ и АС. То есть это угол ВАО = 60°.
б) Аналогично, угол между скрещивающимися прямыми АВ и А1D1 равен углу между пересекающимися прямыми АВ и АD., то есть углу ВАD.
Поэтому, так как АВСD - прямоугольник, то искомый угол - ∠ВАD = 90°.
Пусть стороны а = 7, в = 8 и с = 10,
тогда наибольший угол находится против стороны с.
По теореме косинусов:
с² = а² + в² - 2·а·в·cosα
100 = 49 + 64 - 2·56·cosα
100 = 113 - 112·cosα
112·cosα = 13
cosα = 13:112 ≈ 0,116