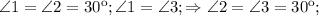 )
) 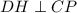 ,
, 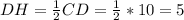 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 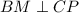 ,
, 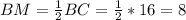 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 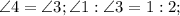
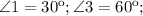 Тогда в ромбе
Тогда в ромбе 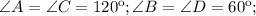
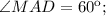 , тогда
, тогда 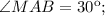 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 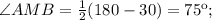
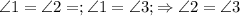 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 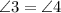 ,
, 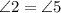 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.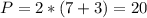 .
.
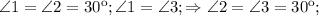 )
) 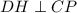 ,
, 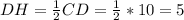 как катет лежащий против угла 30 в треугольнике CHD.
как катет лежащий против угла 30 в треугольнике CHD. 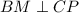 ,
, 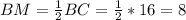 как катет лежащий против угла 30 в треугольнике BMC.
как катет лежащий против угла 30 в треугольнике BMC. 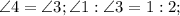
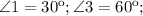 Тогда в ромбе
Тогда в ромбе 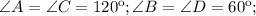
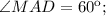 , тогда
, тогда 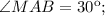 Треугольник BAM равнобедренный, АВ=АМ, тогда
Треугольник BAM равнобедренный, АВ=АМ, тогда 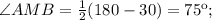
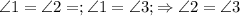 , треугольник MCD равнобедренный, MD=CD=3,
, треугольник MCD равнобедренный, MD=CD=3, 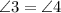 ,
, 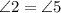 , как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.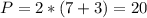 .
.
Биссектриса внутреннего угла треугольника (любого) делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
Рассмотрим треугольник АВС.
ВК - биссектриса и делит АС на отрезки
АК=15 и СК=20.
Отношение этих отрезков 15:20=3:4
Следовательно, АВ:ВС=3:4
Пусть коэффициент отношения сторон будет х.
Тогда АВ:ВС=3х :4х
Коэффициент х найдем по т. Пифагора из треугольника АВС.
АС²=АВ²+СВ²
1225=25х²
х²=49
х=7
АВ=3·7=21
СВ=4·7=28
Биссектриса делит сторону АD на отрезки АЕ и DE
Проведем параллельно АВ из Е прямую ЕМ.
Получили четырехугольник АВМЕ,
в котором ВЕ - его диагональ и биссектриса угла МЕА ( параллельные прямые и секущая ВЕ).
АВМЕ- квадрат со стоной, равной ВА=21
АЕ=АВ=21
DE=28-21=7
ответ: Биссектриса делит сторону прямоугольника на отрезки 21 и 7.