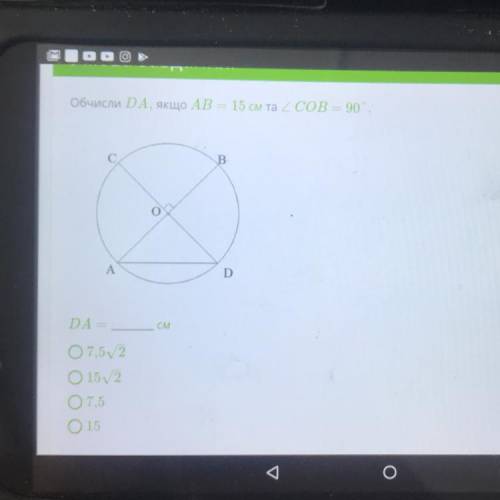
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
(a;b) = |a| * |b| * cost
Если векторы перпендикулярны, то косинус угла между ними будет равен нулю (cos90 = 0), следовательно:
(a;b) = 0
Таким образом мы выяснили, что у перпендикулярных векторов скалярное произведение равно нулю.
Найдем скалярное произведение. Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат
(a;b) = x*(-1)+(-4)*4 = -x-16
Чтобы найти неизвестную переменную, приравняем скалярное произведение к нулю и решим полученное уравнение.
(a;b) = 0
(a;b) = -x-16
-x-16 = 0
x = -16
ответ: -16