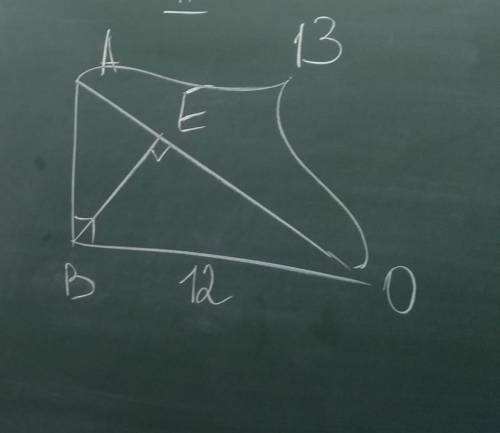
Рисунок во вложении, хотя можно вполне обойтись без него.
1) Найдем вторую сторону основания параллелепипеда из формулы площади основания. Т.к. он прямоугольный, основание - прямоугольник.
S=a*8=40
а=S:8=40:8=5 см
2) Найдем высоту параллелепипеда из формулы объема.
V=S·h
h=V:S
h=240:40=6cм
Площадь боковой поверхности равна произведению высоты на периметр основания:
Sбок=h·2(a+b)
Sбок=6·2·(8+5)=156 см²
Площадь полной поверхности параллелепипеда равна сумме площадей двух его оснований и боковой поверхности:
Sполн= 2·Sосн +Sбок
Sполн=80+156=236 см²
Диагональ можно найти с теоремы Пифагора ( см. рисунок)
Для этого нужно сначала вычислить диагональ основания АС.
Диагональ АС1 параллелепипеда равна
АС1=√(АС²+С1С²)
Можно воспользоваться теоремой:
Квадрат диагонали параллепипеда равен сумме квадратов трех его линейных измерений.
АС1²=АВ²+ВС²+С1С²=8²+5²+6²=125
АС1=√125=5√5 см
-----------------------------------------
№2
Объем прямоугольного параллелепипеда равен произведению высоты на площадь его основания или произведению трех его измерений. Что одно и то же.
V=a·b·c
Об основании известно, что его периметр Р равен 40 см.
Р=2(а+b)
Ни а, ни b не известны, но их длину можно найти.
Пусть ширина основания а, тогда его длина ( по условию) а+4
40=2·(а+а+4)=2а+2а+8=4а+8
4а=40-8=32 см
а=8 см
b=8+4=12 см
Высоту найдем из площади боковой поверхности, которая равна произведению высоты на периметр основания:
Sбок=hP
h=Sбок:Р
h=400:40=10 см
V=a·b·c=8·12·10=960 см³

Объяснение:
1) <BCA - смежный с углом 110°, значит <BCA=180-110=70°. Значит <BCA=<BAC => △ABC - равноб.
2) <BAC - смежный с углом 100°, значит <BAC=180-100=80°. <BCA=<80° как вертикальные. Значит <BCA=<BAC => △ABC - равноб.
3) BD=BE => △DBE - равноб. => <BDE=<BED. По условию <BDE=<BAC, <BED=<BCA => <BAC=<BCA => △ABC - равноб.
4) AD=CD, => △ADC равноб. <ADB=<CDB => DB - бисс, высота и медиана. Но это также значит что она точно медиана и высота для △ABC (для этого треугольника она тоже перпендикулярна и делит AC пополам) => △ABC - равноб. (Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным)
5) <AEB=<CEB как смежные с равными углами <AED=<CED. Для тр-ков AEB и CEB сторона EB общая, а <ABE=<CBE по условию. => △AEB =△CEB по 2му признаку. => AB=BC =>△ABC - равноб.
6) AE=EC => △AEC - равноб. По условию AD=DC, значит ED - медиана и высота, проходящая через точку B. Значит и для △ABC она будет медианой и высотой => △ABC - равноб. (как в 4й задаче)
7) AD=DC => △ADC - равноб. По условию <ADE=<CDE, значит DE - биссектриса, а значит и медиана и высота для стороны AC. Значит и для △ABC она будет медианой и высотой. => △ABC - равноб. (как в 4й задаче)
8) хз
9) Если я правильно понял, по условию AE=FC, ED=DF. Рассмотрим тр-ки AFD и CED. У них AD=AE+ED, CD=DF+FC, и исходя из условия следует, что AD=CD. Угол <ADC у них общий, а ED=DF => △AFD=△CED по 1му признаку. => <AFD=<CED => смежные с ними углы равны <AFC=<CEA. Также из рав-ва этих тр-ков следует, что <DCE=<DAF. По условию, AE=FC => △CFB=△AEB по 2му признаку. => AB=BC => △ABC - равноб.