
Відповідь:
Пояснення:
1. В прямокутному трикутнику один з кутів = 90°, а сума всіх кутів = 180°. Виходячи з цього невідомий кут х=180°-90°-47°=43°
Відповідь: 43°
2. Знайдемо суміжний кут зовнішнього кута 180°-117°=63°. В прямокутному трикутнику один з кутів = 90°, а сума всіх кутів = 180°. Виходячи з цього невідомий кут х=180°-90°-63°=27°
Відповідь: 63° та 27°
3. В цій задачі скористаємося теоремою Піфагора, щоб знайти другий катет:
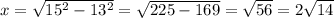
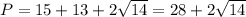 см
см
4. Оскільки із означення вписаного в коло прямокутного трикутника відомо, що радіус описаного кола дорівнює половині гіпотенузи, то гіпотенуза в даній задачі дорівнює відомому катету збільшеному в д рази.
Знайдемо кут протилежний відомому катету х:
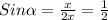
Один кут = 30°. Оскільки це прямокутний трикутник, то прямий кут = 90°, а третій кут = 180°-90°-30°=60°
Відповідь: кути трикутника 30°, 60°, 90°
5. Оскільки дотична із радіусом утворюють кут 90°, то утворюється прямокутний трикутник АОМ, в якому потрібно знайти гіпотенузу ОМ.
Третій кут в трикутнику буде дорівнювати 60°, оскільки 180°-90°-30°=60°.
За теоремою Синусів
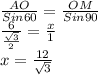
Кут АОС=ВОМ, бо вони вертикальні, а вертикальні кути рівні між собою.
Кут АОМ=СОВ, бо вони вертикальні, а вертикальні кути рівні між собою.
Нехай ∠СОВ+∠ВОМ+∠АОМ=286°.
Суміжними називаються два кути, у яких одна сторона спільна, а дві інші є продовженням одна одної.
Сума суміжних кутів дорівнює 180°.
∠СОВ+∠ВОМ=180°, бо вони суміжні.
∠АОМ+∠АОС=180°, бо вони суміжні.
Виходить, що сума всіх кутів, що утворилися в результаті перетину прямих дорівнює 360°:
∠СОВ+∠ВОМ+∠АОМ+∠АОС=180°+180°
∠СОВ+∠ВОМ+∠АОМ+∠АОС=360°
Оскільки ∠СОВ+∠ВОМ+∠АОМ=286°, виходить
286°+∠АОС = 360°
∠АОС=360-286
∠АОС=74°.
Виходить, що ∠АОС=∠ВОМ=74°.
Тепер оскільки ∠СОВ+∠ВОМ=180°, то
∠СОВ+74°=180°
∠СОВ=180°-74°
∠СОВ=106°.
Виходить, що ∠СОВ=∠АОМ=106°.
Відповідь: два кути по 74° та два кути по 106°.