Пусть ABCD –ромб, т. О – точка пересечения диагоналей, а EFKM –созданный четырехугольник. Пусть диагонали ромба равны a и b соответственно, а сторона его равна с. Тогда площадь ромба равна ab.
Рассмотрим треугольники AOB и EFB – они подобные, из их подобия имеем, что
AB/AO=EB/ES (S – точка пересечения диагонали ромба со стороной четырехугольника)
c : a/2 = c/2 : x
откуда
x=a/4, то есть ES=a/4 и EF=a/2
Аналогично анализируя подобные треугольники OBC и SBF показываем, что FK=b/2
Так как EFKM-прямоугольник, то его площадь равна FK*EF, или
a/2*b/2=ab/4
так как ab=48 из условия задачи, то ab/4=12, то есть площадь EKFM = 12
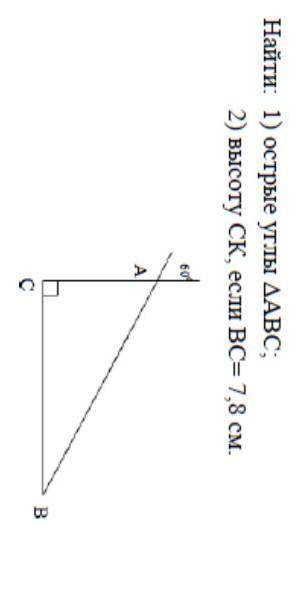
1)угол САВ = 60°, угол АВС = 30° 2) 3,9
Объяснение:
1)
Внешний угол = углу САВ = 60° (как вертикальные)
Сумма острых углов треугольника 90°, значит угол АВС = 90° - 60° = 30°
2)
Проведём высоту СК.
Треугольник СКВ - прямоугольный, угол КВС = 30°, ВС - гипотенуза, ВС = 7,8
Катет, лежащий против угла в 30° равен половине гипотенузы, значит СК = 7,8 ÷ 2 = 3,9