ответ, проверенный экспертом
4,3/5
14
Andr1806
профессор
4.5 тыс. ответов
27.3 млн пользователей, получивших
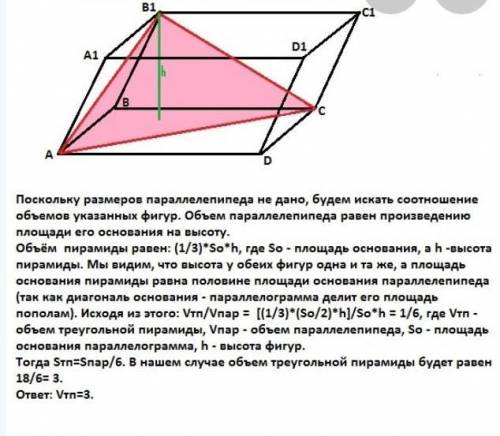
Поскольку размеров параллелепипеда не дано, будем искать соотношение объемов указанных фигур. Объем параллелепипеда равен произведению площади его основания на высоту.
Объём пирамиды равен: (1/3)*So*h, где So - площадь основания, а h -высота пирамиды. Мы видим, что высота у обеих фигур одна и та же, а площадь основания пирамиды равна половине площади основания параллелепипеда (так как диагональ основания - параллелограмма делит его площадь пополам). Исходя из этого: Vтп/Vпар = [(1/3)*(So/2)*h]/So*h = 1/6, где Vтп - объем треугольной пирамиды, Vпар - объем параллелепипеда, So - площадь основания параллелограмма, h - высота фигур.
Тогда Sтп=Sпар/6. В нашем случае объем треугольной пирамиды будет равен 18/6= 3.
ответ: Vтп=3.
Площадь поверхности прямоугольного параллелепипеда S=2⋅(ab+bc+ac), где а, b, с — его измерения. Площадь поверхности равна S=2⋅(3⋅4+3⋅5+4⋅5)=94 (см2). Тогда площадь поверхности параллелепипеда S'=2⋅((X+3)(X+4)+(X+3)(X+5)+ +(X+4)(X+5))=6X2+48X+94=S+54=148 (см2). Так что
6X2+48X+94=148
X2+8X-9=0, X=-9 или X=1. Корень X=-9 не подходит, Значит, Х=1.
Так что