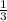BK=
. Значит, DK=2NK=2. Считаем площадь равнобедренного ADC=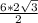
=6. Получаем, наконец, площадь полной поверхности: 3+3*6=21 (площадь основания плюс площади трех боковых граней).
. И наконец, V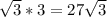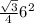=9
=9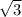
. Идем дальше. Чтобы найти площадь боковой грани ADC (хотя все три равны) надо найти высоту треугольника ADC - DK. Для этого рассм. треуг. DNK. В нем угол DKN=60. Значит, KDN=180-90-60=30. Т.е. в нем DK=2NK (катет, противолежащий углу 30 гр., равен половине гипотенузы). Где возьмем NK? Из равностороннего ABC, где BK - медиана и высота, а значит ВК=
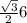=3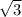. А NK=
АВ=(-5-2; 3+6) = (-7; 9)
СД=(1-4; -3+3.2) = (-3; 0.2)