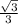1) Так как угол MNO = 60°, а стороны MO=ON как радиусы, то треугольник MNO - равнобедренный и углы OMN и MNO равны друг другу (60°)
В сумме эти углы дают 120°, значит третий угол MON будет равен 180°-120° = 60°. Значит треугольник MON - разносторонний и сторона MN равна радиусу. Диаметр равен двум радиусам:
D=2R=2MN=2*5,4=10,8см
2) Угол MNR равен сумме углов MNO и ONR , то есть: 60° + 90° = 150°
3) Аналогично рассмотрим треугольник OKL , так как KL = MN , то точно так же треугольник OKL является равносторонним, а значит все его углы равны по 60° => угол OKL = углу NKL = 60°
Объяснение:
В условии, очевидно, ошибка: треугольник АВС с такими сторонами не существует, так как любая сторона треугольника меньше суммы двух других сторон, а 6 > 4 + 1.
Эта задача на тему "Подобие треугольников" . Решим ее для ВС = 7 см.
АВ : MK = 4 : 8 = 1/2
AC : MN = 6 : 12 = 1/2
BC : KN = 7 : 14 = 1/2
Значит ΔАВС подобен ΔMKN по трем пропорциональным сторонам.
Сумма углов треугольника равна 180°, значит
∠С = 180° - (∠А + ∠В) = 180° - (80° + 60°) = 180° - 140° = 40°
В подобных треугольниках напротив сходственных сторон лежат равные углы:
∠N = ∠С = 40°,
∠K = ∠В = 60°,
∠M = ∠А = 80°.
это наверно
Определите косинус угла между треугольником A B1C и плоскостью основания куба ABCDA1B1C1D1 со стороной 1.
Объяснение:
Нужно найти двугранный угол В₁АСВ.
В кубе все грани квадраты. Диагональ квадрата равна √(1²+1²)=√2 , половина диагонали 0,5√2. Пусть О-точка пересечения диагоналей основания.
Диагонали квадрата взаимно перпендикулярны , значит ОВ⊥АС. Тк. проекция ОВ⊥АС ,прямой лежащей в плоскости , то и наклонная В₁О⊥АС. Поэтому ∠В₁ОВ-линейный угол двугранного В₁АСВ.
ΔВВ₁О- прямоугольный , tg∠В₁ОВ=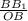
, tg∠В₁ОВ= 
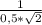=√2.
1+tg²∠В₁ОВ=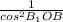
, 1+√2²=
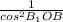,cos∠B₁OB=
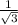, cos∠B₁OB=