
ответ: Ѕ=h₁•h₂/sinα
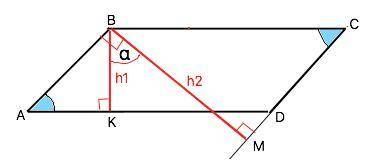
Объяснение: На приложенном рисунке - АВСD- параллелограмм; ВК и ВМ - его высоты.
Из условия ВК=h₁; BM=h₂, угол КВМ=α.
По одной из формул площадь параллелограмма равна произведению соседних сторон на синус угла между ними.
S(ABCD)=AB•АD•sin(BAD).
Высоты параллелограмма перпендикулярны двум его противоположным сторонам.⇒
Треугольники АВК и ВСМ - прямоугольные.
Сумма острых углов прямоугольного треугольника равна 90°, поэтому в ⊿ АВК ∠АВК=90°-∠ ВАК. Но ∠АВМ =90°, ⇒
∠АВК =90°-угол α ⇒
90°-угол ВАК=90°-угол α. ⇒
∠ ВАК =α.
Противоположные углы параллелограмма равны.
Из ⊿ АВК h₁=AB•sinα ⇒ AB=h₁:sinα
Из⊿ СВМ h₂=BC•sinα ⇒ BC=h₂:sinα
Ѕ(ABCD)=AB•BC•sinα=(h₁:sinα)•(h₂:sinα)•sinα=h₁•h₂/sinα.
117/117, 126/126, 59/59, 127/117
Объяснение:
проверено на собственном опыте
правильно на 1000000000000000000%