ответ: 14,4 см.
Объяснение:
"Стороны треугольника равны 36см, 25см и 29см. Найти высоту треугольника проведенную к меньшей стороне."
***
S=ah, где а- основание, h-высота проведенная к основанию а.
По теореме Герона
S=√p(p−a)(p−b)(p−c) , где S – это площадь треугольника; a, b, c – стороны треугольника; p – это полупериметр треугольника. : p=(a+b+c)/2.
***
a=36см b=25 см с=29 см.
р=(36+25+29)/2= 90/2=45;
S=√[45(45-36)(45-25)(45-29)]=√45*9*20*16=√129 600=360 см².
***
По формуле S=ah находим h:
h=S/a, где а=25 см.
h=360/25=14,4 см.
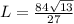
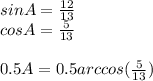
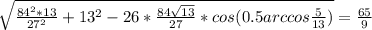
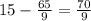
1) Т.к. угол 45 градусов, то h=r. По теореме Пифагора:
h^2+r^2=√10^2. Отсюда h^2=r^2= 10/2 , h=r=5
2) S(бок)=пи*r*L=пи*5*√10
3) V=1/3*пи*r^2*h= 1/3*пи*25^2*5=125пи/3