k=36ПV²/Sполн³
Найдем объем параллелепипида:
V=14*7*5=490 (м³)
Найдем площадь полной поверхности:
Sполн=2(ab+bc+ac)=2(14*7+14*5+5*7)=406
подставим в формулу:

ответ:1. Если KM = NJ, ML = JR, __М= J__, то ΔKML=ΔNJR по первому признаку- по двум сторонам и углу между ними
2. KM = NJ, ML = JR,_KL=NR_, то ΔKML=ΔNJR по третьему признаку-по трем сторонам.
3. KL = NR, ∡ K = ∡ N, _∡ L= ∡ R, то
ΔKML=ΔNJR по второму признаку-по стороне и двум прилежащим углам.
4. KL = NR, ∡ K = ∡ N,_KM=NJ__ , то ΔKML=ΔNJR по первому признаку- по двум сторонам и углу между ними
5. ∡ M = ∡ J, ∡ L = ∡ R, _ML =NR_ , то ΔKML=ΔNJR по второму признаку-по стороне и двум прилежащим углам.
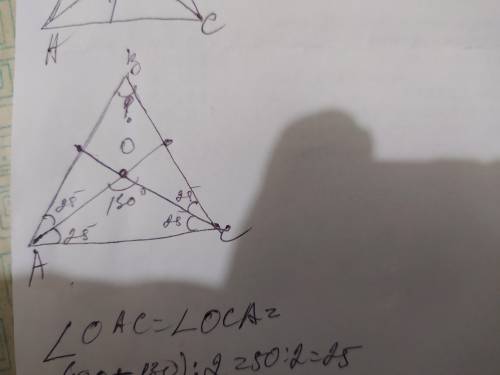
ответ: угол В=80
Объяснение: рассмотрим ∆АОС. Он тоже является равнобедренным, поскольку биссектрисы проведены из равных углов. Теперь вычислим углы ОАС и ОСА. Биссектрисы углов А и С
делят их пополам. Сумма углов в треугольнике равна 180° и поэтому:
180- 130=50. Сумма этих углов=50. Так как они равны: 50÷2=25. Угол ОАС= углу ОСА=25°. Так как угол А и С разделяют биссектрисы, то угол ВАО равен углу ВСО и тоже равны 25°. Следовательно угол А= углу С=50°. Теперь найдём угол В. Угол В = 180-50-50=80
ПАРАЛЛЕЛЕПИПЕД +ПИРАМИДА
V₁=14*7*5=490
V₂=1/3*S*h=1/3*14*7*5=490/3
Vдома=490+490/3=1960/3≈653
S₁=2*(7*5+5*14)=2*(35+70)=210
радиус описанной окружности около основание пирамид≈7,8
боковое ребро≈9,3 (25+60,84=85,84)
высота боковой грани1=6,1
S₂=0,5*14*6,1≈42,7
высота боковой грани2=8,6
S₂=0,5*7*8,6≈30,1
S=210+2*42.7+2*30.1=210+85.4+60.2≈356
k=(36π*653²)/356³=48201273/45118016≈1.07