ответ: Даны треугольники АВС и А1В1С1 в которых стороны АС и А1С1, высоты ВН и В1Н1 и медианы ВМ и В1М1 равны.
Прямоугольные треугольники НВМ и Н1В1М1 равны по 4-му признаку равенства, так как у них гипотенузы (ВМ и В1М1) и катеты (ВН и В1Н1) равны (дано). => HM=H1M1 и <BMH=<B1M1H1. Значит равны и углы ВМС и В1М1С1 как смежные с равными.
АМ=МС=А1М1=М1С1 как половины равных отрезков АС и А1С1.
Треугольники АВМ и А1В1М1 равны по двум сторонам (АМ=А1М1, ВМ=В1М1) и углу между ними (<BMH=<B1M1H1 - доказано выше) => АВ = А1В1.
Треугольники ВМС и В1М1С1 равны по двум сторонам (МС=М1С1, ВМ=В1М1) и углу между ними (<BMС=<B1M1С1 - доказано выше) => ВС = В1С1.
Тогда треугольники АВС и А1В1С1 равны по трем сторонам, что и требовалось доказать.
Объяснение:
все розписано в поясненні
Объяснение:
є два випадки
1 випадок коли кут при вершині більше кута при підставі
а ми знаємо що в рівнобедреному трикутнику кути при підставі рівні на 51 градус
Також ми знаємо що ,,сума кутів трикутника дорівнює 180 градусам,,
Звідси складаємо рівняння
(х+51)+х + х=180
3х=180-51
3х=129
х=129/3
x=43 це кути при основі
43 + 51=94 це кут при вершині
2 випадок коли кут при підставі на 51 градус більше кута при вершині звідси 2 рівняння:
2 (х+51) + х=180
3х=180-102
3х=78
х=78/3
х=26 це кут при вершині
26 + 51=77 це кути при підставі
16 см.
Объяснение:
Площа квадрата визначається по формулі: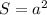 
, де а - сторона квадрата.
Площа прямокутника визначається по формулі: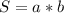 
, де a і b - сторони прямокутника.
===================================
Знаючи з умови, що сторона квадрата a = 12 см, можемо знайти й площу квадрата, й площу прямокутника (бо з умови площі фігур рівні).
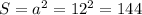см².
==================================
Також нам відома одна сторона прямокутника: a = 9 см. Знаючи площу S прямокутника ми підставляємо відому сторону у формулу площі прямокутника і шукаємо другу сторону:
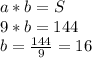см - друга сторона прямокутника.
Даны треугольники АВС и А1В1С1 в которых стороны АС и А1С1, высоты ВН и В1Н1 и медианы ВМ и В1М1 равны.
Прямоугольные треугольники НВМ и Н1В1М1 равны по 4-му признаку равенства, так как у них гипотенузы (ВМ и В1М1) и катеты (ВН и В1Н1) равны (дано). => HM=H1M1 и <BMH=<B1M1H1. Значит равны и углы ВМС и В1М1С1 как смежные с равными.
АМ=МС=А1М1=М1С1 как половины равных отрезков АС и А1С1.
Треугольники АВМ и А1В1М1 равны по двум сторонам (АМ=А1М1, ВМ=В1М1) и углу между ними (<BMH=<B1M1H1 - доказано выше) => АВ = А1В1.
Треугольники ВМС и В1М1С1 равны по двум сторонам (МС=М1С1, ВМ=В1М1) и углу между ними (<BMС=<B1M1С1 - доказано выше) => ВС = В1С1.
Тогда треугольники АВС и А1В1С1 равны по трем сторонам, что и требовалось доказать.
Объяснение: