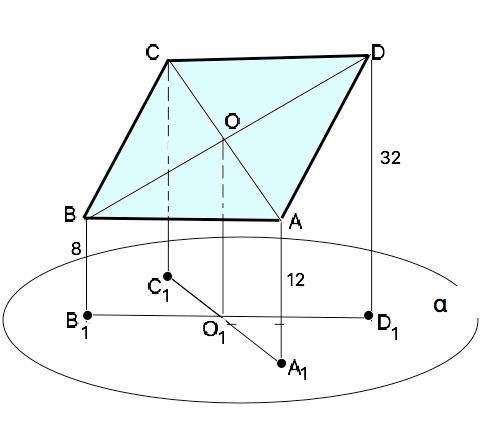
Параллелограмм ABCD не пересекает плоскость α. Через вершины A, B, C и D паралелограма проведены параллельные прямые, которые пересекают плоскость α в точках A1, B1, C1 и D1 соответственно. Найдите длину отрезка CC1, если AA1 = 12 см, BB1 = 8 см, DD1 = 32 см
ответ: 28 см
Объяснение: Параллельные прямые, соединяющие противолежащие вершины параллелограмма с плоскостью α, диагонали и их проекции образуют в пространстве между параллелограммом и плоскостью α две трапеции: АСС1А1 и ВDD1В1 с общей средней линией ОО1, которая соединяет точку пересечения О диагоналей АВСD с ее проекцией О1 на плоскости α
Длина средней линии трапеции равна полусумме оснований.
ОО1=(ВВ1+DD1):2=(8+32):2=20 см =>
СС1+АА1=ОО1•2=40
СС1=40-АА1=40-12=28 см
1. 2
2. Наклонная - AC
Проекция - BC
3. длине перпендикуляра, проведенной от данной точке к прямой
4. ⊥
5. одну и только одну
6. Наклонные прямые - AF, AE
Проекции наклонных - BF, BE
Перпендикулярные прямые - AB, EF
Расстояние от точки A до прямой m - длина AB
7. AC и BO перпендикулярны между собой, AB - наклонная
8. 137 или 43
9. EF - AE - BE - CE - DE
Поблагодарить можно в профиле ;D
Объяснение: