Первая задача решается без вариантов, повторять ее решение нет необходимости.
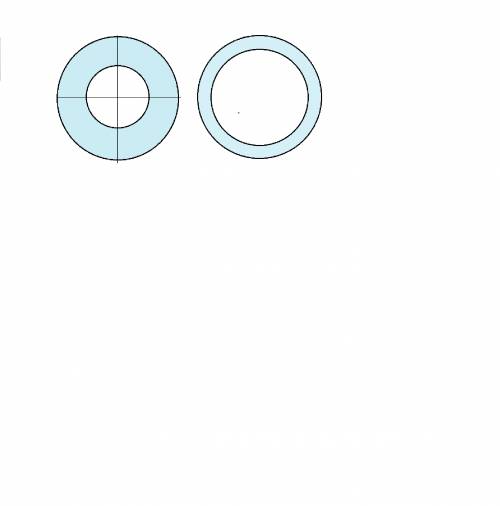
У второй задачи возможны два варианта решения.
Первый - когда площадь внутреннего круга относится к площади кольца как 1:3
Найдем площадь исходного круга:
S=πr²=36π
Тогда 3/4 этой площади занимает кольцо, 1/4- внутренний круг.
36π:4=9π- площадь внутреннего круга
S=πr²=9π
r²=9
r =3
-----------------------
Второй вариант - площадь кольца относится к площади внутреннего круга как 1:3
Тогда площадь кольца 9π,
а площадь внутреннего круга
9π*3=27π
S=πr²=27π
r²=27
r=3√3
Объяснение:
Т.к. противолежащие ребра равны, получается AB=CD=1, AA1=DD1=2. По теореме Пифагора: AD1=√(1²+2²)=√5. Аналогично СD1=√5. AC=√(1²+1²)=√2. Рассмотрим ΔACD1: Он равнобедренный, т.к. AD1=CD1=√5. Соответственно , высота этого треугольника (назовем её D1M), проведенная к основанию АС и будет являться искомым расстоянием от точки D1. В равнобедренном треугольнике высота, проведенная к основанию, является и медианой, поэтому AM=CM=(√2)/2. Теперь по т. Пифагора можно найти катет D1M ΔD1MA: D1M=√(AD1²-AM²)=√((√5)²-((√2)/2)²)=√(5-1/2)=√4.5
3)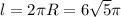
ответ: 5п
4)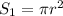
ответ: 3