Не верное утверждение Г.
Объяснение:
А) Прямоугольные треугольники с соответственно равными острыми углами (а даже и с одним, так как второй - прямой) ПОДОБНЫ. Отношение площадей подобных фигур равно квадрату коэффициента подобия (отношению линейных размеров). Значит отношение гипотенуз равно √(2/3). Утверждение верное.
Б) Диагональ трапеции делит ее на два треугольника с одинаковой высотой, следовательно их площади относятся, как их основания, к которым проведена эта высота. Утверждение верное.
В). Медиана треугольника делит треугольник на два треугольника, у которых равны и основания, и высоты. Значит и их площади равны. Утверждение верное.
Г). Периметры равновеликих треугольников в общем случае НЕ равны. (Предыдущий пример с медианой, когда треугольник не равнобедренный - периметры разные). Утверждение НЕ верное.
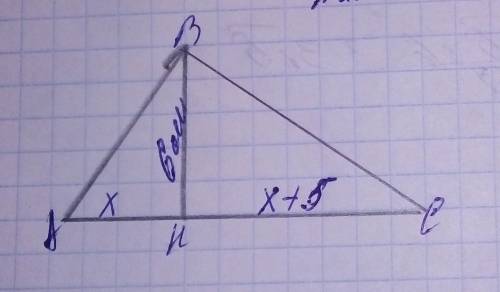
1) рассмотрим АВС- прямоугольный С=90, СН=6см - высота к гипотенузе АВ ,
пусть АН=х, НВ=х+5
исходя из подобия в прямоугольном треугольнике имеем трАВС~CBH~ACH по 2 углам , следовательно АН/СН=НС/НВ х / 6= 6 / х+5 х(х+5)=36 х1=4,х2=-9( не удовлетвояет), отсюда АН=4см, НВ= 9см , АВ=13 см
2) по тПифагора АС=√ (AH^2+HC^2) AC=2√13cm CB= √ (CH^2 +HB^2) CB=√117cm
3) S=1/2 ab S1/S2 =4*3/9*3=4/9
Объяснение: