ответ: 21 (ед. длины)
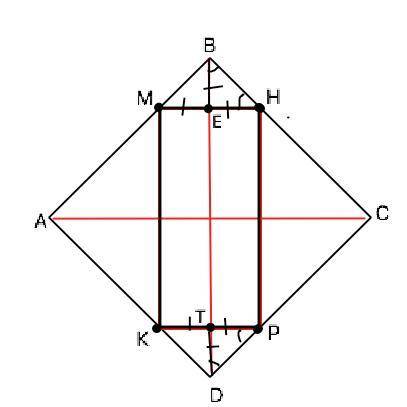
Объяснение: Поскольку стороны вписанного прямоугольника параллельны диагоналям квадрата, диагональ ВD квадрата делит периметр прямоугольника на две равные половины ТКМЕ и ТРНЕ. Как известно, диагонали квадрата делят его углы пополам. При этом угловые треугольники МВН и КDР – равные прямоугольные равнобедренные, в которых ВЕ=ЕМ=ЕН и TD=ТК=РТ. Заметим, что МК+МЕ+ТК=DВ=10,5 - это длина половины периметра прямоугольника. Полный периметр прямоугольника КМНР=2•10,5=21 ( ед. длины)
Дано: трапеция ABCD ∠D=45° AB=9 cм AD=17 см
Найти:ВС
Решение: нам надо дополнить рисунок и из прямоугольной трапеции сделать прямоугольный треугольник( дорисовать 2 прямые из точки B и С) В итоге получится прямоугольный треугольник, у которого один из углов равен 45°
Второй угол так же будет равен 45°, и отсюда следует, что получившийся треугольник равнобедренный с основанием HD ( H- это точка которую ты достраивали в самом начале решения)
HA=AD=17cм HB=17-9=8 cм
Теперь будем рассматривать маленький треугольник HBC
Он тоже равнобедренный и прямоугольный( один угол= 45°, а значит и второй будет равен 45°, потому что сумма всех углов в треугольнике 180°)
HB=BC=8 cм
P.S. Я пыталась написать всё как можно подробнее, чтобы всё было понятно
186 см²
Объяснение:
Дано: КМРТ - трапеция, МК⊥КТ, МК=12 см, РТ=13 см. МТ - биссектриса. Найти S(КМРТ).
∠КТМ=∠РТМ по определению биссектрисы
∠РМТ=∠МТК как внутренние накрест лежащие при МР║КТ и секущей МТ, значит ΔМРТ - равнобедренный, МР=РТ=13 см.
Проведем высоту РН=МК=12 см.
КН=МР=13 см.
ΔРТН - прямоугольный, РТ=13 см, РН=12 см, значит по теореме Пифагора ТН=√(169-144)=√25=5 см
КТ=КН+ТН=13+5=18 см.
S=(МР+КТ):2*РН=(13+18):2*12=186 см²