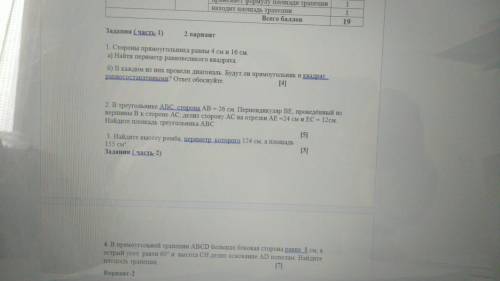
ответ: 25π (дм); 156,25π (дм²).
Объяснение: Для начала обратим внимание, что нам неизвестна гипотенуза.
Теорема Пифагора: сумма квадратов длин катетов равна квадрату длины гипотенузы.
⇒ c²=a²+b² ⇒ c=√(a²+b²)=√(15²+20²)=√(225+400)=√625=25 (дм).
НО можно было не вычислять поскольку есть такое понятие пифагорова тройка, которая содержит пифагоровые числа, удовлетворяющие соотношению Пифагора.
Поэтому мы могли сразу написать по табличке, что:
| a | b | c |
| 15 | 20 | 25 |
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Т.к. AC - диаметр окружности с центром в точке О ⇒ R=25/2=12,5 (см).
Сразу найдём теперь и длину окружности, и площадь круга.
C=2π12,5=25π (дм); S=π12,5²=156,25π (дм²).
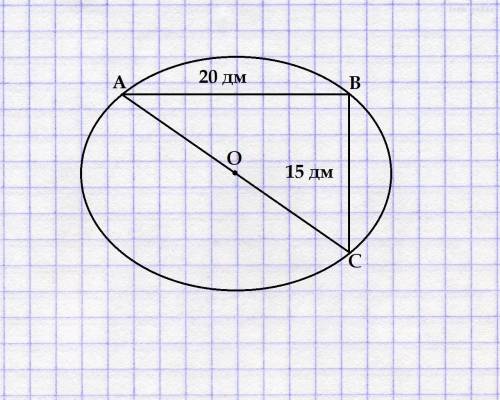
В равнобедренном треугольнике высоты, проведенные к основанию и боковой стороне. равны соответственно 10 и 12 см. Найти длину основания.
ответ: 15 см.
Объяснение:
Пусть данный треугольник АВС (АВ=ВС), высоты ВМ и АК равны 10 и 12 см соответственно.
Прямоугольные треугольники АКС и МВС подобны по общему острому углу С.
Из подобия ВМ:АК=МС:КС
Примем КС=у, МС=х.
Тогда х:у=10:12, откуда у=1,2 х.
ВМ - не только высота. но и медиана р/бедренного ∆ АВС.
АС=АМ+СМ=2х
Из ⊿ АКС по т.Пифагора АС²=КС²+АК²
4х²=144+1,44х²
Для удобства сократим обе стороны уравнения на 4.
х²=36+0,36х² ⇒
х²=56,25 ⇒х=7,5
АС=2х=15 см.