abc - равнобедренный треугольник, тк ав=ас=6. значит углы асв и авс равны между собой. найдём их: abc=acb = (180 - bac)/2 = (180-60)/2 = 60. то есть все углы у треугольника по 60. значит он равносторонний , и все стороны равны 6.
пусть точка e - середина bc. be=ec=3. найдём ае, который является и высотой и меридианой по теореме пифагора (если я не ошибаюсь с названием): ае = корень из (ас^2 - be^2) = корень из (36-9) = корень из (25) = 5.
теперь рассмотри треугольник dae. он прямоугольный (ad также перпендикулярно плоскости треугольника, как и bp. то есть ad образует прямой угол с любым отрезком или прямой, которые принадлежат плоскости треугольника. угол dae - прямой.)
опять же по теореме пифагора найдём гиппотенузу de:
de= корень из (ae^2 + da^2) = корень из (25+9) = корень из (36) = 6
ответ: de=6
ответ: Не верьте громоздким готовым формулам, они отучают думать
Объяснение:
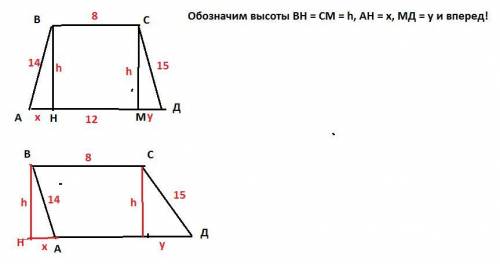
Трапеции бывают разные. Вот если мы применим рисунок со стандартной трапецией, то выяснится, что она не существует.
неизвестная будет отрицательная и прочие неприятности. Но на втором рисунке тоже трапеция, так как АД||ВС, а две другие стороны не параллельны. Вот его мы и решим.
Когда мы провели две высоты мы от основания отрезали отрезок
что у = АД - 8+х или у=4+х Это первое уравнение.
Из прямоугольных треугольников на рисунке выразим высоту, не спеша вдумчиво и применяя теорему святого Пифагора:
Из ВНА будет h² = AB² - x²
Из СМД будет h² = CД² - у² и так как левые части равны, приравняем и правые части АВ²-х² = СД² -у² или подставив значения боковых сторон 14²-х² = 15²-у² а отсюда уже
у²-x²=225-196 = 29 уравнение. Решив систему этих уравнений (я расписывать это здесь не буду, нудно) мы получим, что х=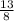
Тогда из треугольника ВНС
h² = 14² -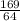 
= 13,9
И это решение верное.
