Question

Найдите объем пирамиды.SABCD правилтная,AS=12,угол SAC=45​

Answer 1

Объяснение:

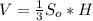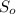Объем пирамиды вычисляется по формуле $V = \frac{1}{3} S_o*H$, где $S_o$ - площадь основы. Пирамида правильная, значит AB = BC = CD = DA = a - сторона основы, а основа - квадрат, значит $S_o=a^2$.

===================

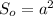Сперва можем найти высоту.

Из прямоугольного ΔASO по соотношениям найдем катет. Знаем гипотенузу и противолежащий катет, а значит:

$sina=\frac{SO}{AS}$ => $SO=ASsina =12*sin45 =12*\frac{\sqrt{2}}{2} =6\sqrt{2}$.

===================

Теперь нужно найти площадь основы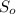 $S_o$, сделать это можно с диагоналей. Диагональ можно найти опять же из треугольника ASO.

Соотношение прилежащего катета и гипотенузы: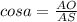 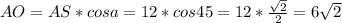$cosa=\frac{AO}{AS}$ => $AO=AS*cosa=12*cos45=12*\frac{\sqrt{2}}{2}=6\sqrt{2}$ - только половина диагонали квадрата; вся диагональ: $AC=2AO=2*6\sqrt{2}=12\sqrt{2}$.

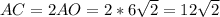Есть формула диагонали квадрата: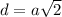 $d=a\sqrt{2}$, из неё выразим сторону => 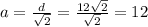$a=\frac{d}{\sqrt{2}}=\frac{12\sqrt{2}}{\sqrt{2}}=12$ - сторона основы.

Найдем площадь основы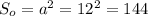 $S_o=a^2=12^2=144$ ед.²

===================

Теперь можем найти объем пирамиды:

$V=\frac{1}{3}S_o*H=\frac{1}{3}S_o*SO=\frac{1}{3}*144*6\sqrt{2} =48*6\sqrt{2}=288\sqrt{2}$ ед.³