Нарисуй правильную пирамиду КАВСД с вершиной в точке К.
Расстояние от точки К до плоскости АВС равно высоте, опущенной из точки К на эту плоскость. Эта высота, обозначим её КО падает в центр основания- квадрата АВСД, которая лежит на пересечении диагоналей квадрата.
Диагональ квадрата равна 2*sqr(2), т.к. сторона квадрата равна 2.
Рассмотрим треугольник АОК. Угол АОК=90 град, АО=sqr(2), т.е. половине диагонали, АК=4 (по условию). По теореме Пифагора находим длину КО:
КО=sqr(4^2-2)=sqr(14)
ответ:sqr(14)
Одна из параллельных прямых пусть будет a и точка, в которой ее пересекает секущая будет A. Другая из параллельных прямых будет b и точка, в которой ее пересекает секущая будет B. Из точки A опустим перпендикуляр на прямую b и получим точку С на прясой b: это расстояние между параллельными прямыми, AC = 12 см по условию. Один из углов, образованных секущей равен 30 градусам, пусть это будет угол ABC. Рассмотрим получившийся прямоугольный треугольник ABC.
Катет AC = 12 см и он лежит против угла в 30 градусов (угол ABC = 30 градусов) и, следовательно равен половине гипотенузы AB.
Составим уравнение: AC = 1/2 * AB;
2 * AC = AB;
2* 12 = AB;
AB = 24.
Расстояние между точками пересечения прямых A и B равно 24 см.
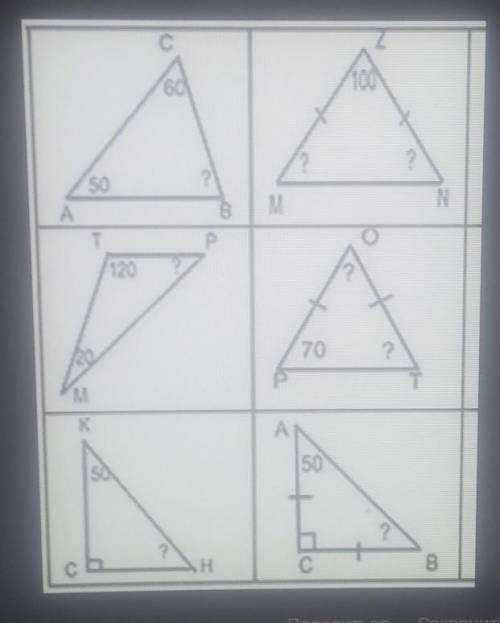
1.180-(50+60)= 70° (угол В)
2.180-100=80 80:2=40°( угол М и N)
3.180-(120+20)=40° (угол Р)
4.70+70=140 180-140=40( угол О). угол Т=70°( равнобедренный поэтому)
5.90-50=40°(угол Н)
6.Рисунок неправильный