Две плоскости пересекаются под углом 60°. Точка М находится на одинаковом расстоянии от этих плоскостей. Найдите расстояние от точки М до линии пересечения этих плоскостей, если расстояние от точки М до каждой плоскости равно 4 см.
ответ: 8 см
Объяснение:
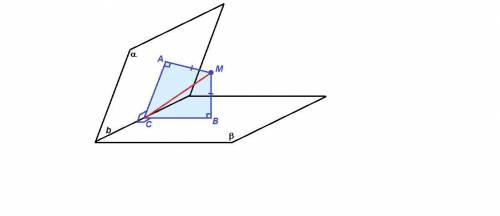
Пусть плоскости α и β пересекаются по прямой b.
Расстояние от точки до плоскости - длина перпендикуляра, проведенного из точки к плоскости.
Проведем МА⊥α и МВ⊥β. По условию МА = МВ = 4 см.
Плоскость (АМВ) пересекает прямую b в точке С.
АМ⊥α, b ⊂ α, значит АМ⊥b,
ВМ⊥β, b ⊂ β, значит ВМ⊥b,
а так как прямая b перпендикулярна двум пересекающимся прямым плоскости (АМВ), то она перпендикулярна и всей плоскости, и каждой прямой, лежащей в плоскости.
Итак, b⊥АС и b⊥ВС, тогда ∠АСВ = 60° - линейный угол двугранного угла между плоскостями.
А так же b⊥МС, значит МС - искомое расстояние от точки М до прямой b.
ΔАМС = ΔВМС по гипотенузе и катету (МА = МВ по условию, гипотенуза МС - общая), значит
∠МСА = ∠МСВ = 1/2 ∠ АСВ = 30°
В прямоугольном треугольнике АМС напротив угла в 30° лежит катет АМ = 4 см, значит
МС = 2АМ = 8 см
Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи.
На рисунку або .
Синусом кута називається відношення протилежного катета до гіпотенузи:
або .
Тангенсом кута називається відношення протилежного катета до прилеглого:
або .
Котангенсом кута називається відношення прилеглого катета до протилежного:
або .
Значення , , , залежать тільки від величини кута.
З означень випливає, що для гострих кутів і прямокутного трикутника (див. рисунок) маємо:
; ;
; ;
, а також , .