В равностороннем треугольнике все углы равны 60°.
Высоты, по свойству высоты равнобедренного треугольника, являются биссектрисами и медианами, и каждая делит его на 2 равных прямоугольных треугольника.
Высота в таких треугольниках является большим катетом, который противолежит углу 60°, сторона равностороннего треугольника- гипотенузой, а меньший катет противолежит углу 30° и равен половине гипотенузы (свойство)
-----------------
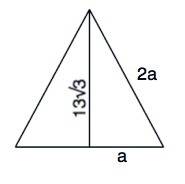
Примем меньший катет (половину стороны) равным а. Тогда гипотенуза (сторона равностороннего треугольника) равна 2а.
По т.Пифагора с²=a²+b² (с- гипотенуза, а и b- катеты)⇒
(2а)²=а²+((13√3)²⇒
3а²=13²•3 ⇒ а=13,
Сторона данного равностороннего треугольника 2а=26 (ед. длины)
или
с=b:sin60°, где с - сторона равностороннего треугольника, b- его высота.
с=(13√3):(√3/2)=26 (ед. длины)
Значит угол DАВ=180 - <ABC=180-120=60°
угол BCD=180 - <CDA=180-30=150°
Проведем из вершины С на основание АD прямую СЕ, параллельную стороне АВ. Получается четырехугольник АВСЕ - параллелограмм (противоположные стороны параллельны), значит равны его противоположные стороны (АВ=СЕ, ВС=АЕ=12) и противоположные углы (<DAВ=<ВСЕ=60°, <АВС=<CЕA=120°).
Рассмотрим ΔCDЕ, у него <DСЕ=<ВCD-<ВCЕ=150-60=90°, значит треугольник прямоугольный.
Найдем катет СЕ=DЕ*sin <CDA=(AD-AE)*sin 30=(20-12)*1/2=8*1/2=4 см
Значит АВ=4см.