
Нарисуем этот треугольник.
Обозначим точки буквами- см.рисунок.
Получились прямоугольные треугольники, высоты в который определяются по формуле высоты равностороннего треугольника
h=(а√3):2
Найдем сторону ВК в треугольнике КВМ
3=(ВК√3):2
(ВК√3)=3*2=6
ВК=6:√3=2√3
По той же формуле найдем АВ
5=(АВ√3):2
АВ√3=5*2=10
АВ=10:√3=(10√3):3
АК=(10√3):3 -2√3=(10√3 -6√3):3=(4√3):3
КН=√3(4√3):3):2=12:6=2см
рисунок - во вложении
----------------------------------------------
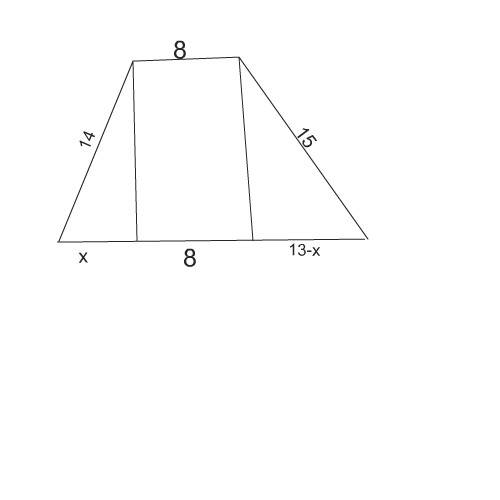
Рисуем трапецию.
Опустим из ее углов при меньшем основании высоты на нижнее основание.
Получили один прямоугольник и два прямоугольных треугольника при боковых сторонах как гипотенузах.
Найдем значение высот и приравняем их.
Для этого отрезок основания при боковой стороне 14 обозначим х, а отреок ( катет) при боковой стороне 15 будет 21-х-8=13-х
14²-х²=15²-(13-х)²
Из этого уравнения найти х, затем из прямоугоьного треугольника с гипотенузой 14 и катетом, равным найденному х, вычислить высоту трапеции.
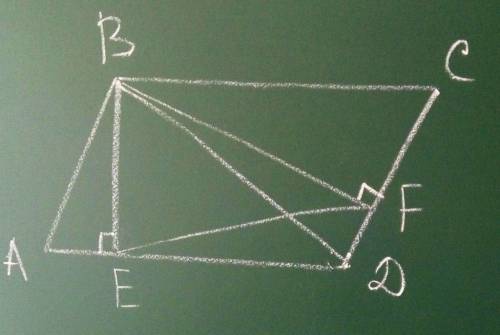
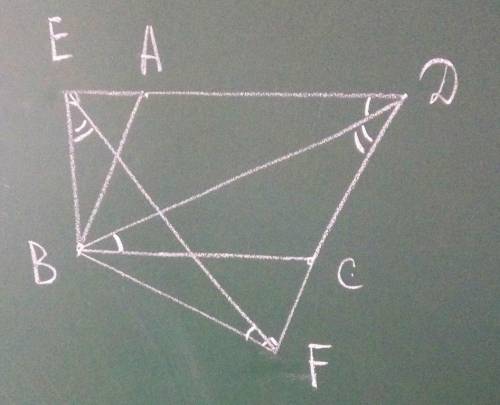
Объяснение:
ABCD-параллелограмм⇒∠C=∠A, AD║BC
∠C=∠A⇒sin∠C=sin∠A
AD║BC⇒∠CBD=∠ADB
BE⊥AD⇒∠BED=90°
BF⊥AD⇒∠BFD=90°
∠BED=∠BFD=90°⇒ точки B,E,F,D лежат на одной окружности с диаметром BD. Тогда по теореме о равенстве вписанных углов имеем ∠BEF=∠BDF, ∠BDE=∠BFE
∠BFE=∠BDE=∠CBD
∠BEF=∠BDC, ∠BFE=∠CBD⇒ΔBEF~ΔBDC ч.т.д.
Из ΔBEF по теореме синусов имеем EF/sinEBF=2R, где R-радиус описанной окружности около ΔBEF⇒ R=0,5BD, так как это та самая окружность которая содержит точки B,E,F,D.
EF/sinEBF=2R⇒EF=2RsinEBF=BDsinC=BDsinA=15·0,4=6
Случаи того что угол В острый или тупой разбираются аналогично.
S=9×12×sin150°
sin150°=sin(180°-30°)=sin30°=1/2
S=9×12×1/2=54см^2