1). Когда мы нарисуем рисунок, то увидим, что это сечная. Отсюда ми уже знаем, что каждий противоположный внутренний угол будет равен противоположеному внутренему улу, така само и со внешнеми углами. Если взять только одну прямую с сечной, то это образуеться вертикальние углы, вместе с их особеностями.
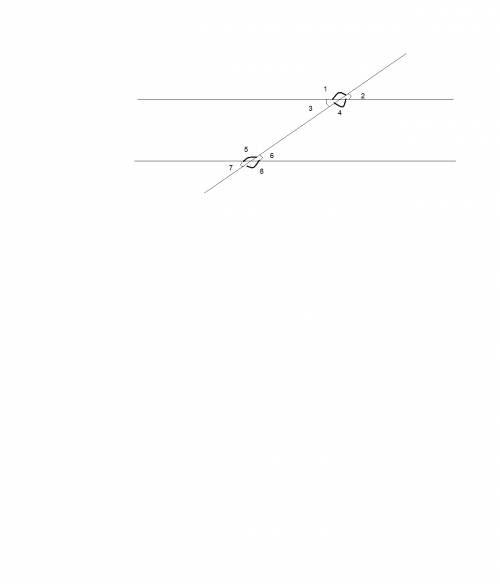
Два сумежных угла будут равны 180гр., отсюда можно зделать вывод, что 80градусам може доривнювати только сума одинаковых углов., отсюда угол 6+угол3=80гр. Так, как углы равны, то угол 3=40гр. Теперь мы можем узнать, скольким градусам равен угол 4: 180-40=140гр.
ответ:1=140; 2=40; 3=40; 4=140; 5=140; 6=40; 7=40; 8=140гр.
2). Так, как треугольник равнобедренный значит и углы при основании будут равны, они становлять 75градусов.
Из треугольника АДС: угол АДС=90, так как это угол при высоте; Угол ДСА=75гр., отсюда угол ДАС=15гр.
ответ:15гр.
Если что то непонятно, спрашивай)))
0) Обозначим одну точку как H, это будет ортоцентр. А другую, как O, это будет центр описанной окружности.
Вспомним два свойства ортоцентра:
1. Точка, симметричная ортоцентру относительно прямой, содержащей сторону треугольника, лежит на описанной около треугольника окружности.
2. Точка, симметричная ортоцентру относительно середины стороны треугольника, лежит на описанной около треугольника окружности и диаметрально противоположна вершине треугольника, противолежащей данной стороне.
1) Построим точку H' симметричную H относительно прямой а. Для этого: проводим полуокружность с центром H и радиусом (p) большим, чем расстояние от H до прямой а. Из точек пересечения полуокружности с прямой, проводим окружности с радиусом (p). Они пересеклись в двух точках, одна H, другая H'.
По свойству ортоцентра (1.) H' лежит на описанной окружности.
2) Проведём окружность с центром в точке O и радиусом OH'. Это и есть описанная окружность. По условию, точки пересечения этой окружности с прямой a, будут вершинами треугольника. Обозначим эти вершины как A и B. Построим сторону AB.
3) Определим середину AB. Для этого: проводим окружности с центрами в точках A и B, с равными радиусами (r), которые больше, чем половина AB. Через точки пересечения этих двух окружностей проводим прямую q. Точку пересечения прямых q и а обозначим как M. Это и есть середина AB.
4) Построим последнюю вершину треугольника C. Проводим прямую k через точки M и H. Точку пересечения k с описанной окружностью обозначим, как H₁. По свойству ортоцентра (2.) точка H₁ диаметрально противоположная точке С. Проводим через точки H₁ и O прямую t, точку пересечения прямой t и окружности обозначим как С. Это и есть последняя вершина.
5) Построим стороны AC и BC треугольника ABC. Задание выполнено.