Объяснение:
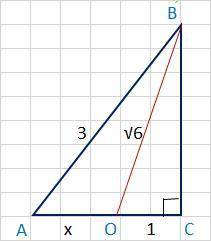
1. ∠С отмечен квадратиком, это означает, что он прямой, т.е ∠С =90°. Значит, ΔАВС и ∠ОВС - прямоугольные
(Гипотенуза - это сторона Δ-ка, лежащая против прямого угла)
2. Теорема, необходимая для решения задач с прямоугольным треугольником:
Квадрат гипотенузы равен сумме квадратов катетов, т.е.
АВ² = ВС² + АС² ( из ΔАВС) и
ОВ² = ВС² + ОС² (из ΔОВС)
3. Решение
а) Рассмотрим ΔОВС.
ОВ² = ВС² + ОС² или
(√6)² = ВС² + 1², откуда
ВС² = 6-1
ВС² = 5
б) теперь обратимся к ΔАВС.
АВ² = ВС² + АС² или
3² = 5 +АС², откуда
АС² = 9 -5 = 4
АС = √4 = 2
Но АС = АО + ОС или
2 = АО + 1
АО = х = 2 -1
АО = х = 1
№2.
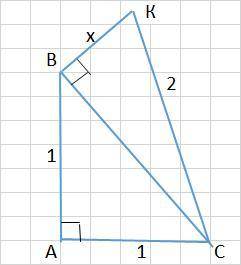
1) ΔАВС - прямоугольный, т.к. ∠А = 90° (прямой)
ВС² = АВ² + АС² (квадрат гипотенузы = сумме квадратов катетов)
ВС² = 1 + 1
ВС² = 2
2) Рассмотрим ΔВКС, он тоже прямоугольный, т.к. ∠КВС = 90° (по условию, рис.)
КС² = ВС² +ВК² или
2² = 2 + х²
х ² = 4 - 2
х² = 2
х = √2
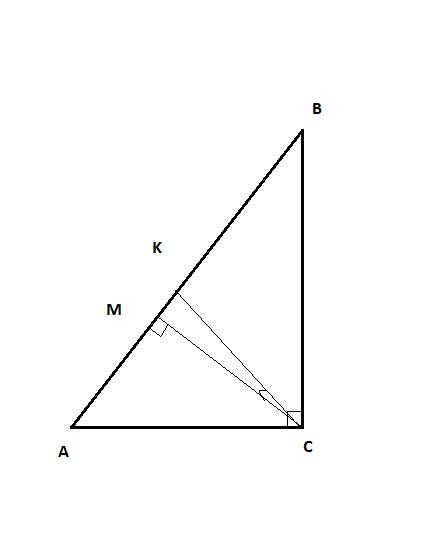
Пусть N лежит на АР так, что MN II BC.
Тогда треугольники ВКР и MNK равны, поскольку у них равны все углы и ВК = КМ.
Поэтому NK = KP, а поскольку NP = AP/2, то КР = АР/4;
Далее, MN = PC/2; но ВР = MN; поэтому ВР = РС/2 = ВС/3;
Теперь применяется (в массовом порядке :) ) известное свойство - если у треугольников высоты к каким-то сторонам равны, то площади относятся, как длины этих сторон.
Если обозначить S площадь АВС, то площадь АРС равна S*2/3;
Площадь АВМ равна S/2; а площадь АКМ (и - между прочим - площадь АВК) равна половине площади АВМ, то есть S/4;
Окончательно, площадь KPCM равна S*2/3 - S/4 = S*5/12; а искомое отношение равно (S/4)/(S*5/12) = 3/5;