НА ПОУЧИ, НЕУЧ!
Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
Коллинеарные вектора
рис. 1
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Найдем их векторное произведение
a × b =
i j k
ax ay az
bx by bz
= i (aybz - azby) - j (axbz - azbx) + k (axby - aybx) =
= i (aynaz - aznay) - j (axnaz - aznax) + k (axnay - aynax) = 0i + 0j + 0k = 0
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
ax = ay .
bx by
Значит:
Вектора a и b коллинеарны т.к. 1 = 2 .
4 8
Вектора a и с не коллинеарны т.к. 1 ≠ 2 .
5 9
Вектора с и b не коллинеарны т.к. 5 ≠ 9 .
4 8
Пример 2. Доказать что вектора a = {0; 3} и b = {0; 6} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
n = by = 6 = 2
ay 3
Найдем значение na:
na = {2 · 0; 2 · 3} = {0; 6}
Так как b = na, то вектора a и b коллинеарны.
Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
ax = ay .
bx by
Значит:
3 = 2 .
9 n
Решим это уравнение:
n = 2 · 9 = 6
3
ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
ax = ay = az .
bx by bz
Значит:
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
n = by = 6 = 2
ay 3
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Так как b = na, то вектора a и b коллинеарны.
Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
ax = ay = az .
bx by bz
Значит:
3 = 2 = m
9 n 12
Из этого соотношения получим два уравнения:
3 = 2
9 n
3 = m
9 12
Решим эти уравнения:
n = 2 · 9 = 6
3
m = 3 · 12 = 4
9
ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Хитрый треугольник со стороной 5 — ни что иное, как египетский треугольник со сторонами 3, 4, 5.
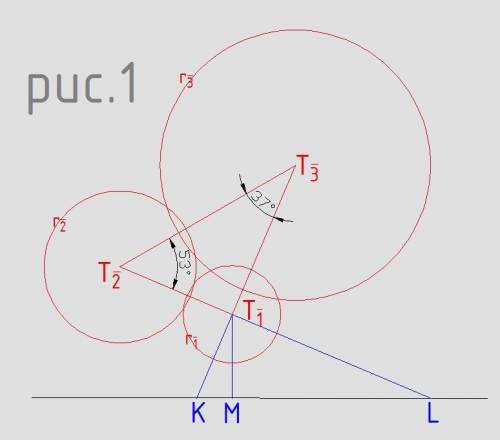
Т₁, Т₂, Т₃ — точки касания шаров исходной плоскости
U₁, U₂, U₃ – точки касания шаров второй плоскости
O₁, O₂, O₃ – центры шаров
Пусть расстояние 3 между точками касания шаров r₁ и r₂, расстояние 4 — между шарами r₁ r₃, расстояние 5 — между шарами r₂ r₃
Рисунок 1 - вид сверху на плоскость с точками касания шаров. Красными окружностями показаны вычисленные радиусы шаров
----------------------------------------
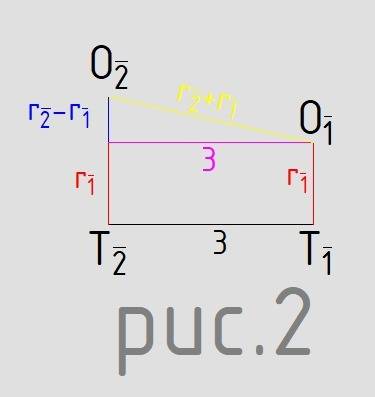
Рассмотрим прямоугольную трапецию T₁T₂O₂O₁ (рисунок 2), образованную точками касания двух шаров и их центрами. Основания этой трапеции — радиусы шаров, наклонная боковая сторона — сумма радиусов,
O₁O₂ = r₁ + r₂
боковая сторона с прямыми углами — это сторона исходного треугольника.
T₁T₂ = 3
Проекция наклонной боковой стороны на основание равна разнице радиусов шаров r₂ - r₁
По т. Пифагора для прямоугольных треугольников в каждой из трёх таких трапеций
(r₂ – r₁)² +3² = (r₂ + r₁)²
(r₃ – r₁)² +4² = (r₃ + r₁)²
(r₃ – r₂)² +5² = (r₃ + r₂)²
r₁² - 2*r₁*r₂ + r₂² + 9 = r₁² + 2*r₁*r₂ + r₂²
r₁² - 2*r₁*r₃ + r₃² + 16 = r₁² + 2*r₁*r₃ + r₃²
r₂² - 2*r₂*r₃ + r₃² + 25 = r₂² + 2*r₂*r₃ + r₃²
4*r₁*r₂ = 9
4*r₁*r₃ = 16
4*r₂*r₃ = 25
из второго
r₁ = 4/r₃
подставим в первое и третье
4*4/r₃*r₂ = 9
4*r₂*r₃ = 25
Перемножим
4*4*4*r₂² = 9*25
8*r₂ = 3*5
r₂ = 15/8
подставим в первое
4*r₁*15/8 = 9
r₁ = 6/5
и подставим в третье
4*15/8*r₃ = 25
r₃ = 10/3
Радиусы шаров определены.
Между пересекающимися плоскостями шары располагаются так, что меньший шар r1 ближе всего к линии пересечения, средний шар r2 дальше, и наибольший ещё дальше r3
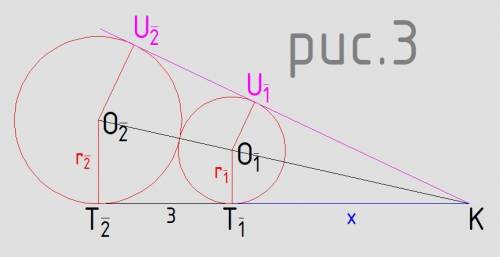
Для трапеции из пункта T₁T₂O₂O₁ продолжим наклонную боковую сторону O₂O₁ до линии пересечения плоскостей. (рисунок 3)
x = Т₁K – расстояние от точки касания меньшего шара до линии пересечения плоскостей по прямой,
Из подобия ΔT₁O₁K и ΔT₂O₂K
x/r₁ = (x+3)/r₂
x*r₂ = (x+3)*r₁
x*15/8 = x*6/5 + 18/5
x*(75 – 48)/40 = 18/5
27x = 18*8
3x = 16
x = 16/3
KT₁ = 16/3
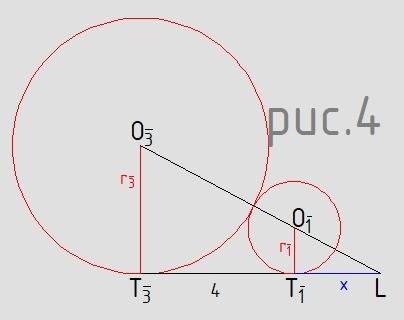
Аналогично для шаров r₁ r₃ рассмотрим трапецию Т₁T₂O₂O₁ и ΔT₁O₁L, ΔT₂O₂L (рисунок 4)
x/r₁ = (x+4)/r₃
x*r₃ = (x+4)*r₁
x*10/3 = x*6/5 + 24/5
x*(50 – 18)/15 = 24/5
32/15*x = 24/5
4/3*x = 3
x = 9/4
LT₁ = 9/4
----------------------------------------------
Найдём высоту треугольника KLT₁
Гипотенуза по т. Пифагора
KL² = KT₁² + LT₁² = (9/4)² + (16/3)² = 4825/144 = 25/144 * 193
KL = 5/12*√193
Площадь через катеты равна площади через гипотенузу и высоту к ней
9/4*16/3 = MT₁*5/12*√193
3*4 = MT₁*5/12*√193
MT₁ = 144/5/√193
----------------------------------------
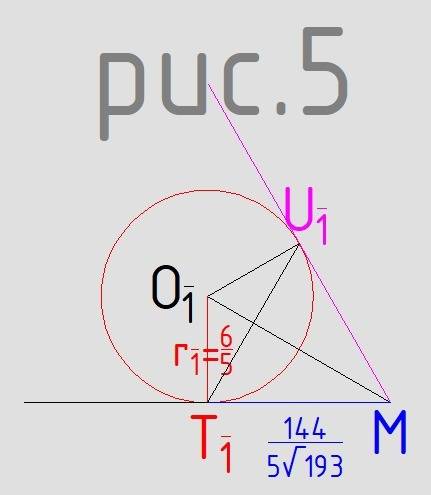
Теперь перейдём в секущую плоскость O₁T₁M (рисунок 5)
∠O₁MT₁ = arctg(6/5/144*5√193) = arctg(√193/24)
Угол между плоскостями
∠O₁MU₁ = 2*arctg(√193/24)
Расстояние между точками касания плоскостей малым шаром
O₁M по т. Пифагора
O₁M² = 36/25 + 144²/(25 *193) = 27684/4825
O₁M = √(27684/4825) = 6/5*√(769/193)
Высота треугольника O₁MT₁ через площадь, площадь через катеты и площадь через гипотенузу и высоту к ней.
6/5 * 144/(5√193) = h*6/5*√(769/193)
144/5 = h√769
h = 144/(5√769)
Расстояние между точками касания плоскостей малым шаром
T₁U₁ = 2h = 288/(5√769)
NK=5*8.8=44
или
mk=1,(36)
nk=0,56(81)