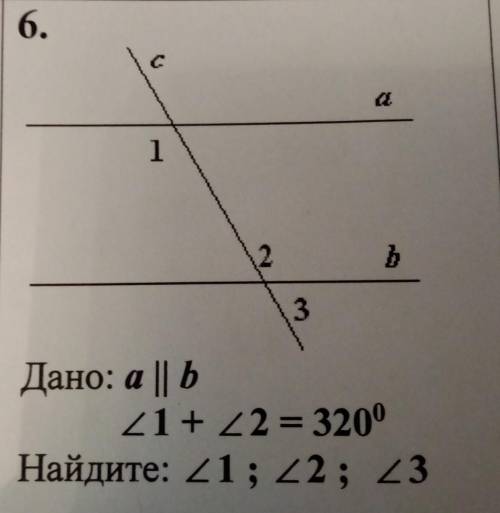
Вектор АМ = (4-(-4); 2-4) = (8; -2).
Уравнение высоты АМ:
х + 4)/8 = (у - 4)/(-2), или в общем виде х + 4у - 12 = 0.
Сторона треугольника АС перпендикулярна этой высоте.
Коэффициенты в уравнении ВС меняются так: -В и А, то есть -4 и 1.
Уравнение АВС: -4х + у + С = 0.
Для определения слагаемого С подставим координаты точки В:
-4*(-4) + (-12) + С = 0, отсюда С = 16 + 12 = 28.
Уравнение ВС: -4х + у + 28 = 0 или 4х - у - 28 = 0.
Так как сторона АС перпендикулярна высоте ВМ, у которой координаты точек по оси Ох совпадают, то АС - горизонтальная линия.
А так как она проходит через точку с ординатой у = 4, то это и есть уравнение стороны АС: у = 4.
Подставим у = 4 в уравнение ВС и найдём координату точки пересечения прямых, это точка С.
4х - 4 - 28 = 0, отсюда х = 32/4 = 8.
ответ: координаты точки С(8; 4).
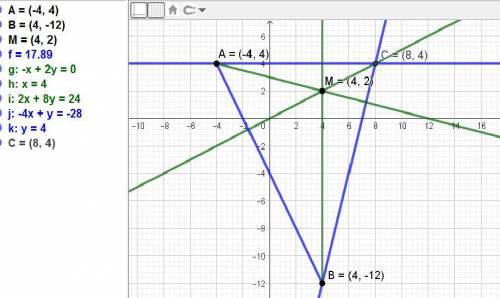
Треугольник с прямым углом - это прямоугольный треугольник.
Так как меньшие стороны "прилегают" к прямому углу, то эти стороны - катеты.
Так как катеты имеют длины 6 см и 8 см, то также такой треугольник - египетский (треугольник с соотношением сторон, равным 3:4:5). Следовательно, гипотенуза равна 10 см (можно также проверить через теорему Пифагора).
Высота, проведённая к большей стороне - высота, проведённая к гипотенузе (так как гипотенуза - самая большая сторона в прямоугольном треугольнике).
Высота, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу.
То есть -
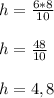
h = 4,8 см.
ответ: 4,8 см.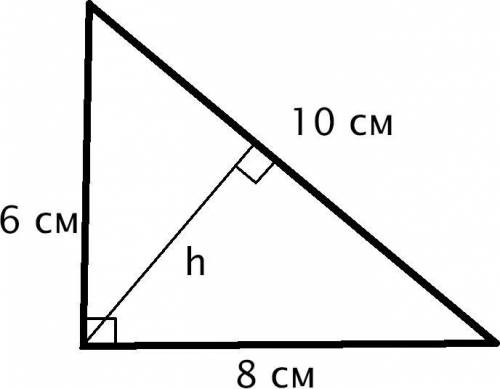
320÷2=160
угол 1 ,угол 2=160°
180-160=20
угол 3=20°