АВСD - равнобокая трапеция, АС и ВD диагонали, по условию они перпендикулярны.
Проведите СК параллельно диагонали ВD. К лежит на продолжении АD. Получится треугольник АСК. Он прямоугольный, потому что угол АСК= углу АОD = 90 градусов. К тому же этот треугольник равнобедренный, потому что в нем СК=АС. FR - основание треугольника.
Проведите высоту этого треугольника с вершины С. Пусть это будет отрезок СМ.
Высота в равнобедренном треугольнике, проведенная к основанию, будет чем ? -медианой. Значит, М - середина АК. СМ = 1/2АК = 1/2(АD + DК)
а DК = ВС, как противоположные стороны параллелограмма ВСКD.
Тогда
СМ = 1/2(а + в)
А средняя линия как раз и равна 1/2(а+в)
Значит, высота равна средней линии
CK=5,9 см
Объяснение:
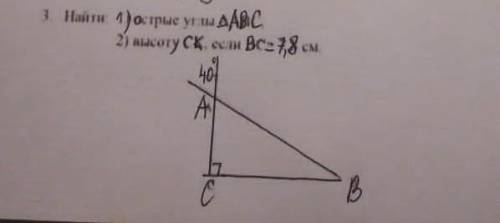
∠CAB=40°, т.к. ∠CAB и угол 40° - вертикальные.
tg∠CAB=BC/AC ⇒ AC=BC/tg∠CAB
Рассмотрим ΔCKA: он прямоугольный, т.к. CK- высота (по условию), сл-но, sin∠CAK=CK/AC ⇒ CK=AC*sin∠CAK
CK=9,3*sin40°=9,3*0,64=5,9 (см)