
Вообще-то есть формулы перехода углов прав. пирамид, от угла наклона α бокого ребра к плоскости основания к углу β наклона боковой грани к плоскости основания, они связаны таким соотношением tgβ=√2*tgα, я эти формулы выводил еще в школе, а сейчас, когда у меня не крепятся файлы, конечно, будет сложно, объяснить, но я попробую.
В основании лежит квадрат. Проекцией бокового ребра к плоскости основания будет половина диагонали квадрата, если сторону обозначить а, то диагональ квадрата равна а√2, а ее половина а√2/2=а/√2, высота пирамиды пусть будет Н, тогда тангенс угла наклона бок. ребра к плоскости основания равен 2Н/а√2=√2*Н/а, теперь разберемся с углом наклона боковой грани к плоскости основания, проведем из основания высоты пирамиды, т.е. из точки пересечения диагоналей квадрата к стороне квадрата перпендикуляр, равный а/2, это проекция апофемы на плоскость основания, которая тоже будет перпендикулярна стороне квадрата по теореме о трех перпендикулярах. тангенс угла наклона бок. грани к плоскости основания равен 2Н/а,
tgα=tg60°=√3, tgβ =√2tg60°=√2*√3=√6, и тогда угол наклона, который мы ищем, равен arctg(√6)
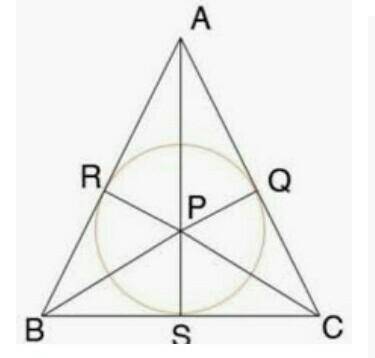
Якщо коло вписане в рівнобедрений трикутник, значить вершини цього трикутника будуть проводити дотичні до кола. Є таке правило: якщо з однієї точки проведено 2 дотичні(це максимум) до кола, то вони будуть рівні до точки дотику. Тобто якщо глянути на малюнок, то побачимо що з кожної вершини проведено дві дотичні, тобто вони будуть рівними. Відомо що AQ = 5, QC = 4. так як це рівнобедренний трикутник то протилежна сторона теж поділена так само. З вершини C проведено 2 дотичні, а значить вони рівні. Тобто CQ = CS = 4 см, те саме з іншої сторони. Тому периметр = 26 см
Объяснение:Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом.
Значит ∠ADC=∠C+∠B ⇒можно составить уравнение:
14х+17=78+(6х+11)
14х-6х=78+11-17
8х=72
х=72:8
х=9°
Значит ∠ADC= 14x+17°= 14·9°+17°=126°+17°= 143°