Дуга AB = 80°
Объяснение:
Дано:
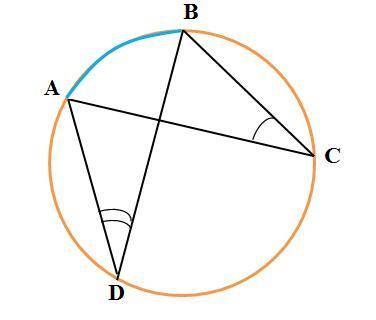
в окружности (см. рисунок)
∠ADB - вписанный угол
∠ACB - вписанный угол
∠ADB+∠ACB=80°
Найти: дуга AB
Решение.
Вписанные углы ∠ADB и ∠ACB опираются на дугу AB.
Далее применим следующие свойства вписанных углов:
Теорема 1. Вписанные углы, опирающиеся на одну и ту же дугу равны.
Теорема 2. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
По теореме 1: ∠ADB=∠ACB. Тогда из ∠ADB+∠ACB=80° следует:
∠ADB+∠ADB=80° или 2·∠ADB=80°.
По теореме 2: дуга AB = 2·∠ADB. Отсюда дуга AB = 2·∠ADB = 80°.
, как диагонали равных квадратов, значит Δ
- равнобедренный, О - середина АС, значит 
- медиана, биссектриса и высота, то есть ⊥
⊥ 
, ⊥ 
, значит ⊥ 
, и перпендикулярна любой прямой этой плоскости, в том числе 
, значит ∠
, - проекция на плоскость АВС и ⊥, значит ⊥ и ∠
Высота h треугольника МВД равна 5√2/cos 45° = (5√2)/(√2/2) = 10 см.
ВД = 10√2.
ответ: S(МВД) = (1/2)*10*10√2 = 50√2 см².