1. Треугольник равнобедренный
2. Существует. По теореме : длина каждой стороны треугольника меньше суммы длин двух других его сторон.
3. Существует по тойже теореме.
5. Решение:
докажем что треугольники КМВ и СОЕ равны.
1) Так как ЕО и КМ перпендикуляры опущенные на гипотенузу ВС , то уголы ЕОС=ВМК - они прямые.
2) Угол АВС равен углу ВСА, так как треугольник АВС равнобедренный.
3) Так как точки К и Е лежат середине боковых сторон и треугольник АВС равнобедренный, то КВ=ЕС.
4) Так как К и Е отмечены на середиах боковых сторон и от них проведены перпендикуляры к гипотенузе ВС, то угол ВКМ равен углу СЕО.
5) Треуголиники КМВ и СОЕ равны (по второму признаку равенства треугольников.
6) Отсюда следует, что КМ=ЕО
Т.к. АД || ВС, а АС секущая к ним, то углы СВД=АДВ и АСВ=САД. Углы ВКС и АКД равны как вертикальные. Тогда треугольники АКД и ВКС подобны по 3-м равным углам, коэффициент подобия по условию равен 2:5. По свойству подобных треугольников отношение высот равно коэффициенту подобия. Из точки К проведем высоту h1 в треугольнике ВКС и высоту h2 в треугольнике АКД.
Из подобия треугольников:
1) ВС:АД=2:5; АД=5ВС/2
2) h1:h2=2:5; h2=5h1|/2
Площадь ВКС=ВС*h1/2. Площадь АКД=АД*h2/2=5ВС/2*5h1/2=25*площадь ВКС/4=25*8/4=50
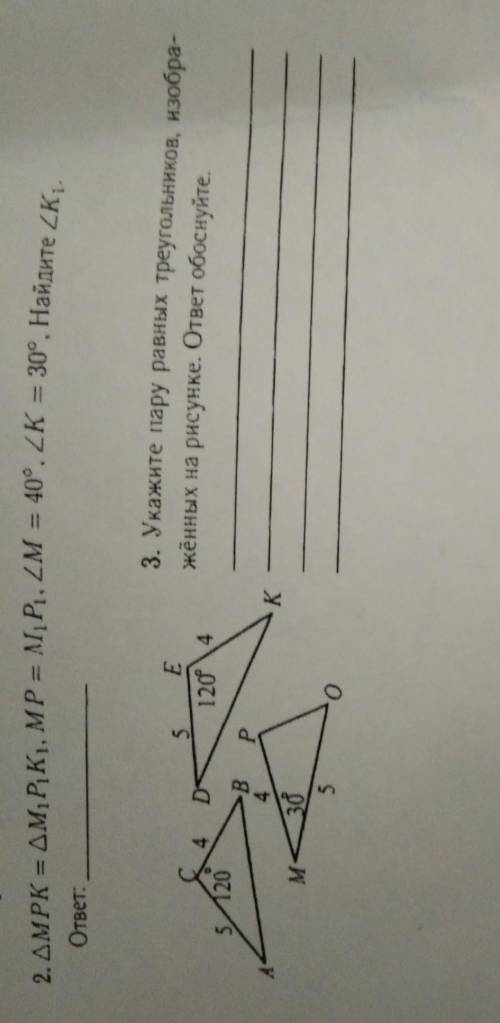
∆MPK=∆M¹p¹k¹=MP=m¹p¹ угол М¹ =40° угол к =30° найдите угол к