
1)
Площадь любого треугольника равна половине произведения высоты на сторону, к которой она проведена.
Формула высоты равностороннего треугольника равна
h=(а√3):2
а=1 м по условию задачи.
S=(1*1√3):2=0,5√3 м²
2)
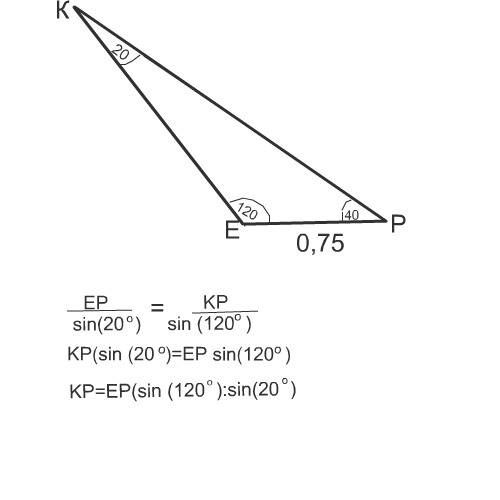
Для решения задачи следует применить теорему синусов. Ход решение дан во вложении, значения синусов найдете по таблице и без труда сделаете вычисления самостоятельно.
3)
Для решения задачи следует применить теорему косинусов:
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Cos(100°) -0.1736
Третья сторона равна корню квадратному из
(1806,25+1,69- 2·55,25· (-0.1736)=42,745 см²
Опустим из вершины к основанию треугольника высоту и получим два прямоугольных треугольника с острыми углами 60° - при основании и 30° - при вершине.
Гипотенуза такого треугольника 1м, меньший катет, как противолежащий углу 30°, равен половине гипотенузы и равен 0,5 м
Высота ( второй катет) находится по теореме Пифагора:
h²=1²-0,5²
h²=1-0,25
h²=0,75
h=(√3):2 м
Теперь по классической формуле площади треугольника найдем площадь равностороннего треугольника со стороной, равной 1м
S=0,5a·h
S=0,5·(√3):2=(√3):4 м²
Для нахождения площади равностороннего треугольника есть специальная формула а²√3:4, так же, как есть формула высоты равностороннего треугольника (а√3):2. Их очень полезно знать наизусть. Но и без этого можно обойтись, конечно. С теоремы Пифагора.
Но знание этих формул сэкономит много времени.
по т синусов
AS/sinD=2R=d
AS^2=(2-0)^2+(-1-0)^2+(3-0)^2=4+1+9=14; AS=√14
по т косинусов можно найти cos<D, но предварительно посчитать оставшиеся стороны
AD^2=(-1-0)^2+(1-0)^2+(1-0)^2=3; AD=√3
DS^2=(2+1)^2+(-1-1)^2+(3-1)^2=17; DS=√17
т косинусов
AS^2=DS^2+AD^2-2*DS*AD*cos<D
14=17+3-2*√17*√3*cos<D
cos<D=6/(2√51)=3/√51=√(3/17)
из основного тождества найду sin<D
sin^2<D+cos^2<D=1
sin^2<D=1-3/17=14/17; sin<D=√(14/17)
d=AS/sin<d=√14:√(14/17)=√17
ответ d=√17