Вравностороннем конусе радиус основания равен 15 см. найти площадь сечения , проведенного через 2 образующие, угол между которыми равен 30 градусов

👇

Увидеть ответ

Ответ:

Galinachlen

06.06.2021

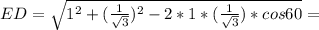
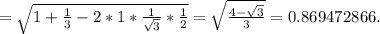
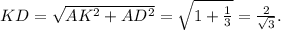
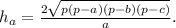
Равносторонний конус - это ПЕРЛ! Это где же его стороны?

Другое дело: конус, осевое сечение которого является равносторонним треугольником. Полагаю, что условие такое.

Решение.

Если радиус основания R = 15см, а осевое сечение равносторонний треугольник, то образующая конуса L и диаметр основания D равны.

L = D = 2R = 30см.

Длина хорды а окружности основания, являющаяся неизвестной стороной треугольного сечения, образованного двумя образующими, , угол между которыми равен 30° может быть найдена из теоремы косинусов.

а² = L² + L² - 2L²·cos30° = 2L²·(1 - cos30°)

а² = 2·30²·(1 - 0.5√3) = 1800·(1 - 0.5√3)

a = 30·√(2 - √3)

Высоту h треугольного сечения, проведунная к стороне а найдём по теореме Пифагора

h² = L² - (0.5a)²

h² = 900 - 450·(1 - 0.5√3) = 450·(1 + 0.5√3) = 225·(2 + √3)

h = 15√(2 + √3)

Площадь сечения

S = 0.5a·h = 0.5· 30·√(2 - √3)·15√(2 + √3) = 225·(4 - 3) = 225(cм²)

4,6(17 оценок)

Ответ:

vipvikaviktoria

06.06.2021

Решение.

L = D = 2R = 30см.

а² = L² + L² - 2L²·cos30° = 2L²·(1 - cos30°)

а² = 2·30²·(1 - 0.5√3) = 1800·(1 - 0.5√3)

a = 30·√(2 - √3)

Высоту h треугольного сечения, проведунная к стороне а найдём по теореме Пифагора

h² = L² - (0.5a)²

h² = 900 - 450·(1 - 0.5√3) = 450·(1 + 0.5√3) = 225·(2 + √3)

h = 15√(2 + √3)

Площадь сечения

S = 0.5a·h = 0.5· 30·√(2 - √3)·15√(2 + √3) = 225·(4 - 3) = 225(cм²)

4,8(7 оценок)

Открыть все ответы

Ответ:

mamarika2001

06.06.2021

а) Постройте плоскость, проходящую через точки K, L и М - для этого надо просто соединить эти точки.

б) Найдите угол между этой плоскостью и плоскостью основания АВС.
Продлим отрезки КМ и KL до пересечения с плоскостью АВС. Для этого достаточно продлить стороны АС и АВ.
Точки пресечения - это Д и Е.
Примем длину отрезка АК за 1.
Из треугольника АКД отрезок АД = 1 / tg 60 = 1 / √3.
Аналогично АЕ = 1 / tg 45 = = 1 / 1 = 1.
Угол ЕАД равен 60 градусов (по заданию).
По теореме косинусов $ED= \sqrt{1^2+( \frac{1}{ \sqrt{3}} )^2-2*1*( \frac{1}{ \sqrt{3} } )*cos60}=$
$= \sqrt{1+ \frac{1}{3} -2*1* \frac{1}{ \sqrt{3} }* \frac{1}{2}} = \sqrt{ \frac{4- \sqrt{3} }{3} } =0.869472866.
$
Находим гипотенузы в треугольниках АКД и АКЕ.
$KD= \sqrt{AK^2+AD^2} = \sqrt{1+ \frac{1}{3} } = \frac{2}{ \sqrt{3} } .$
КЕ = √(1²+1²) = √2 (острые углы по 45 градусов).
Теперь определены 3 стороны в треугольнике КЕД, угол наклона которого к плоскости АВС надо найти.
Для этого двугранный угол между основой и треугольником КДЕ надо рассечь плоскостью, перпендикулярной их линии пересечения ЕД.
Находим высоты в треугольниках АЕД и КЕД по формуле:
$h _{a} = \frac{2 \sqrt{p(p-a)(p-b)(p-c)} }{a} .$
АЕ ДЕ АД   p 2p S =
1   0.8694729    0.5773503   1.2234116   2.446823135     0.25
haе        hде      hад
0.5        0.57506   0.86603

КЕ    ДЕ   КД   p 2p S =
1.4142136 0.869473   1.154701   1.719194    3.43839   0.501492
hке    hде hкд
0.7092 1.15356   0.86861.
Отношение высот hде и  hде  - это косинус искомого угла:
cos α = 0.57506 / 1.15356 = 0.498510913.
ответ: α = 1.048916149 радиан = 60.09846842°.

4,7(87 оценок)

Ответ:

myagkixmatveeva

06.06.2021

Пирамида правильная, следовательно, в основании лежит правильный треугольник.
Площадь полной поверхности - площадь основания+площадь боковой поверхности.
Площадь основания S(o) вычислим по формуле:
S=(а²√3):4
S(о)=(9√3):4
Площадь боковой поверхности Sб - по формуле
Sб=Р*(апофема):2
Основание высоты МО правильной пирамиды перпендикулярно основанию и лежит в центре вписанной окружности/
Апофему МН найдем из прямоугольного треугольника МОН.
Т.к. грань наклонена к плоскости основания под углом 45, высота пирамиды равна радиусу вписанной в правильный треугольник окружности, а апофема МН, как гипотенуза равнобедренного прямоугольного треугольника, равна с=а√2, т.е.ОН*√2
МО=ОН.
ОН=r=(3√3):6=(√3):2
МН=(√3):2)*√2=(√3*√2):2
Р=3*3=9
Sб=9*(√3*√2):2):2=9*(√3*√2):4 см²
Sполн=(9√3):4+(9*√3*√2):4
Sполн=9√3)(1+√2):4 или 2,25*(1+√2) ≈ 5,43 см²
----
bzs*
Сторона правильной треугольной пирамиды 3 см, а угол между боковой гранью и основанием пирамиды раве