Объяснение:
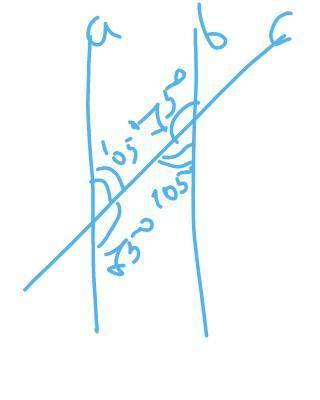
Есть такое правило: накрест лежащие углы равны. Т.е. если мысленно провести две линии от двух разных углов к двум другим так, что они образуют крест, углы, на концах этих линий, будут равны. Тобишь угол 2=75(т.к. он накрест лежащий). Угол 2(или три -- они всё равно равны) смежен с соседним(составляют вместе развёрнутый угол). Соответственно для того, чтобы вычислить углы 1 и 4 нужен из 180(развернутого угла) вычесть угол 2 или 3(75 градусов). Мы получаем 105. Следующим пунктом можно проделать то же самое с неизвестным углом, либо вычислить его по правилу накрест лежащего угла(с 1 или 4 в зависимости от того, какой вы находили).
Если мой ответ показался Вам полным и доступным , выберете его лучшим.
ответ: 144; 36°
Объяснение:
1. Находим сторону ромба по теореме Пифагора. Она будет равна корню квадратному из суммы квадратов половин диагоналей:
AB=√(d1/2)²+(d2/2)²=√(2/3)²+2²=√40/9=2,1м
2. Находим синус угла треугольника, образованного половинами диагоналей и боковой стороной:
sinα=(ВD/2)/АВ=2/2,1=0,95
3. Находим угол α и этот угол будет равен половине угла ВАD
α=arcsin0,95=72°
4. Находим ∠ВАD
∠ВАD=∠α*2=72*2=144°
5. Сумма углов в ромбе, прилегающих к одной стороне равна 180°,
Значит ∠АВС=180-∠ВАD=180-144=36°
Противоположные углы в ромбе равны между собой.
Боковое ребро L = 12см,
Высота пирамиды: Н = L·sin60° = 12·0.5√3 = 6√3(cм)
Радиус описанной окружности треугольного основания: R = L·cos60° = 12·0.5 = 6(см)
Сторона а правильного треугольника, лежащего в основании: а = R·√3 = 6√3(см)
высота треугольного основания: h = a·sin 60° = 6√3·0.5√3 = 9(cм)
Площадь основания Sосн = 0.5a·h = 0.5· 6√3 · 9 = 27√3(cм²)
Апофема (высота боковой грани) А² = L² - (0.5a)² = 144 - 27 = 117
A = 3√13(cм)
Площадь боковой грани: Sгр = 0,5а·А = 0,5·6√3·3√13 = 9√39(см²)
Площадь боковой поверхности
Sбок = 3·Sгр = 3·9√39 = 27√39(см²)
Площадь поверхности пирамиды S = Sосн + Sбок = 27√3 + 27√39 =
= 27√3(1 + √13) (см²)
Объём пирамиды: V = 1/3 Sосн ·Н = 1/3 · 27√3 · 6√3 = 162(см³)