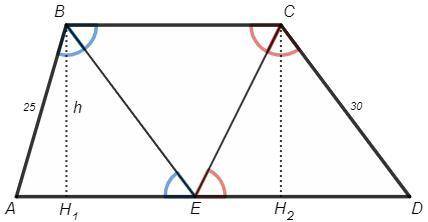
AB=25, CD=30 - боковые стороны трапеции; h=24 - высота.
1) B, C - тупые углы при одном основании
BE, CE - биссектрисы, E лежит на AD.
Биссектриса внутреннего угла при параллельных отсекает равнобедренный треугольник.
BAE, CDE - равнобедренные, AB=AE=25, CD=DE=30
AD=AE+DE =25+30=55
Опустим высоты из вершин B и С. По теореме Пифагора найдем отсеченные отрезки большего основания:
AH1=√(25^2-24^2)=7
DH2=√(30^2-24^2)=18
BC=AD-AH1-DH2 =55-7-18=30
S(ABCD)= (AD+BC)/2 *h =(55+30)/2 *24 =1020 (см^2)
2) B, D - противоположные тупые углы
В этом случае биссектриса угла D пересекает биссектрису угла B в точке B (несовпадающие прямые могут иметь только одну общую точку).
BCD - равнобедренный, BC=CD=30
AD=30-18+7 =19
S(ABCD)= (AD+BC)/2 *h =(19+30)/2 *24 =588 (см^2)
1) Сумма внутренних углов треугольника 180.
B=180-35-45=100
2) Внешний угол треугольника равен сумме внутренних, не смежных с ним.
С=110-40=70
3) Сумма острых углов прямоугольного треугольника 90.
B=90-30=60
4) Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна 360.
Найдем внешний угол при вершине A
360-120-110=130
Внешний и внутренний углы являются смежными, 180.
A=180-130=50
5) Найдем внутренний угол при вершине С. Внешний и внутренний углы являются смежными, 180.
С=180-125=55
В равнобедренном треугольнике углы при основании равны, A=C=55
B=180-A-C =180-55*2=70
Из этого невнятного условия можно (с трудом) догадатся, что все боковые ребра пирамиды наклонены к основанию под 60 градусов (если это не так - поправьте :)).
В основании равнобедренный прямоугольный треугольник с гипотенузой 4, радиус описанной окружности равен 4/2 = 2. Площадь основания равна 2*4/2 = 4.
Высота пирамиды, радиус описанной окружности и боковое ребро образуют прямоугольный треугольник с углом 60 градусов (противолежащим высоте пирамиды).
Это следует из того, что все ребра равнонаклонены. Пусть М - проекция S на АВС. Тогда все прямоугольные треугольники SMA, SMB, SMC равны (по катету и противолежащему острому углу) => S равноудаленa от вершин => проекция вершины S на АВС равноудалена от вершин А, В, С, то есть АМ = ВМ = СМ - радиус окружности, описанной вокруг АВС.
Таким образом высота пирамиды Н = 2*tg(60) = 2*корень(3).
Объем пирамиды (1/3)*4*2*корень(3) = 8*корень(3)/3
Следует понимать :)) что в этой задаче вершина S проектируется на основание АВС точно в середину М гипотенузы ВС, то есть боковая грань SBC перпендикулярна основанию АВС, и высота пирамиды SM лежит в этой боковой грани :))