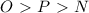- всё это конечно углы.
меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
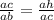
теперь подставим наши значения в эту пропорцию:
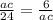
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см
Так же треугольники КАО и KTM подобны . Из подобия треугольников получаем
5x/(5x+y)=y/(23/16 + y) .
Так как
KT^2+TM^2=KM^2
(5x+y)^2+(y+23/16)^2=KM^2 ;
KO^2=(5x)^2+y^2
OM^2=y^2+(23/16)^2
отудого KM=KO+OM = √((5x)^2+y^2) + √(y^2+(23/16)^2)
ставим в уравнение
(5x+y)^2+(y+23/16)^2=KM^2 ;
(5x+y)^2+(y+23/16)^2 = (√((5x)^2+y^2) + √(y^2+(23/16)^2))^2
решаем систему
{(5x+y)^2+(y+23/16)^2 = (√((5x)^2+y^2) + √(y^2+(23/16)^2))^2
{5x/(5x+y)=y/(23/16 + y)
получаем отудого x=23/80
значит AK=5*23/80=23/16