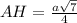Дан угол АВС=86°.Через точку А проведена прямая параллельная прямой ВС и пересткающая бессектрису угла в точке М.Найдите углы треугольника АВМ и сумма его
Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.
A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
Свойство 1. Площадь фигуры является неотрицательным числом.
Свойство 2. Площади равных фигур равны.
Свойство 3. Если фигура разделена на две части, то площадь всей фигуры равна сумме площадей образовавшихся частей.
Еще нужна фигура, которую мы примем за эталон для измерения площади, ¾ единицу площади. При этом не следует забывать, что уже имеется единица измерения длины.
Свойство 4. За единицу измерения площади принимается площадь квадрата со стороной, равной 1 единице длины.
Другими словами, площадь квадрата со стороной, равной 1 единице длины, равна 1 единице площади, или 1 квадратной единице. Например, площадь квадрата со стороной 1 метр равна одному квадратному метру
Фигуры, имеющие равные площади, называтся равновеликими.
Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.
A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
ответ: