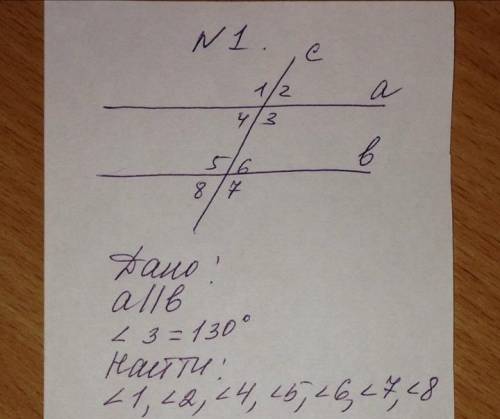
Высота этого треугольника, опущенная на гипотенузу из вершины прямого угла, равна 9:6·2= 3 см
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Найдем эти отрезки, обозначив один из них х, другой 6-х:
9=х(6-х)
9=6х-х²
3²= x *(6-x)
х²-6х+9=0
Решив это квадратное уравнение, найдем два одинаковых корня х=3
Следовательно, отрезки, на которые высота делит гипотенузу, равны, и треугольник - равнобедренный.
Высота равна 3, половина гипотенузы=3.
Из прямоугольного треугольника с катетами 3 и 3 найдем боковую сторону ( катет исходного треугольника)
х²=3²+3²=18
х= √18=3√2
Катеты равны 3√2
Проверка:
Площадь найдем половиной произведения катетов:
S= (3√2)·(3√2):2=9·2:2=9 cм²
<1 = 130, <2 = 50, <4 = 50, <5 = 130, <6 = 50, <7 = 130, <8 = 50
Объяснение:
1) <1 = <3 (как вертикальные углы)
<1 = 130
2) <2 + <3 = 180 (как смежные углы)
<2 = 180 - <3 = 50
3) <2 = <4 (как вертикальные углы)
<4 = 50
4) <3 = <5 (как накрест лежащие)
<5 = 130
5) <6 + <3 = 180 (как внутренние одностроронние)
<6 = 50
6) <7 = <5 (как вертикальные углы)
<7 = 130
7) <6 = <8 (как вертикальные углы)
<8 = 50