
20,5
Объяснение:
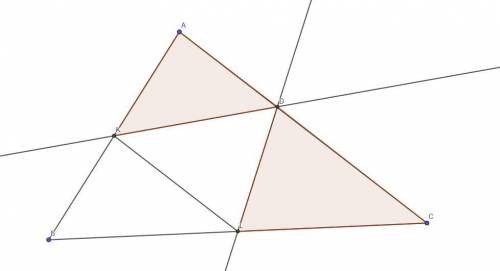
Точки K и L — середины сторон AB и BC соответственно.
KL - это средняя линия.
Средняя линия параллельна противолежащей стороне и равна ее половине.KL || AC
∠AKD=∠LKD - по условию∠KLD=∠DLC - по условию∠LKD=∠KDA - как накрест лежащие углы при KL || AC и секущей KD
∠KLD=∠LDC - как накрест лежащие углы при KL || AC и секущей LD
Значит, ∠AKD=∠LKD=∠KDA и ∠KLD=∠DLC=∠LDC
⇒ ΔAKD и ΔCDL - равнобедренные ⇒ KA=AD, LC=CD
Значит, KA=AD=BK, LC=CD=BL
AC=AD+CD=(1/2)·AB + (1/2)·BC=(1/2)·(AB+BC)=(1/2)·41=20,5
Сторона ромба равна 6,6 см.
Объяснение:
Ромб - это параллелограмм, у которого все стороны равны, а противоположные стороны параллельны: RK ║ MP.
1) Рассмотрим ΔRNK и ΔMNP.
∠NKR = ∠NPM - как соответственные углы при параллельных прямых RK и MP и секущей NP.
∠N - общий.
Следовательно ΔRNK подобен ΔMNP по двум углам (первый признак подобия).
В подобных треугольниках соответственные стороны пропорциональны:
Пусть сторона ромба равна х см. Тогда RK = x см, NК = (8,8-х) см.
Умножим обе части равенства на 26,4:
х=3(8,8-х)
х=26,4-3х
4х=26,4
х=6,6
Сторона ромба равна 6,6 см.