Соч по за 4 четверть 7 класс. суммативного оценивания за 4 четверть 1 вариант 1. ас - касательная к окружности. хорда ав равна радиусу окружности. найдите угол между касательной и хордой. ) [3 2. равнобедренный треугольник abc (ab-bc) вписан в окружность. угол при вершине в равен 40°. найдите величины дуг ас, ав и ви. [4 3. в окружности с центром в точке о к хорде ав, равной радиусу окружности, перпендикулярно проведен диаметр cd. диаметр cd и хорда ав пересекаются в точке т. длина отрезка ав равна 8 см. a) постройте рисунок по условию ; b) определите длину хорды ав; c) определите длину диаметра cd; d) найдите периметр треугольника oab [4 4. в прямоугольном треугольнике aob (zo = 90°) ab = 12, zain = 30°. c центром в точке а проведена окружность. каким должен быть ее радиус, чтобы: a) окружность касалась прямой во, b) окружность не имела общих точек с прямой во, c) окружность имела две общие точки с прямой во? [4 5. постройте треугольник авс по следующим данным: ab = 5 см, ас = 6 см, 2 а=40*. в полученном треугольнике постройте биссектрису yrna b. [5
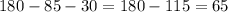
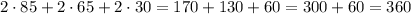
Диагонали прямоугольника равны между собой.
При пересечении диагоналей образуются равнобедренные треугольники.
Рассмотрим один из них, вершина которого составляет 120 градусов.
Находим углы при основании этого треугольника: (180 -120) :2 = 30градусов
угол 30 гр лежит против меньшей стороны прямоугольника, принимаем меньшую сторону пр-ка за Х.
Теперь рассмотрим треугольник, образованный одной диагональю.
Он -прямоугольный, в котором меньший катет лежит против угла в 30 гр.и равен Х, следовательно гипотенуза(диагональ) = 2Х
2Х+Х = 36 (по условию)
3Х = 36
Х = 12
2Х = 24
ответ: 24 см - диагональ прямоугольника.