Такую задачу можно делать с теоремы о пропорциональных отрезках, но при этом нужно проводить дополнительные линии, а мне делать это лень. Поэтому воспользуемся теоремой Менелая. Советую перед разбором решения ознакомиться с формулировкой этой теоремы. А заодно и с теоремой Чевы. А если посмотрите и теорему Ван-Обеля, вы будете подкованы на 100%.
Кстати, удобно сначала воспользоваться теоремой Чевы. Поскольку чевианы PM, RK и QN пересекаются в одной точке, справедливо равенство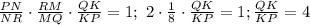 .
.
То есть в QK четыре части, а в KP одна часть. Следовательно, в PQ=PK+KQ пять частей, а тогда 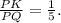
Для нахождения второго отношения воспользуемся теоремой Ван-Обеля. Поскольку чевианы PM, RK и QN пересекаются в точке S, то
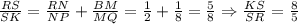
Для нахождения третьего отношения применим теорему Менелая к треугольнику PRS и прямой NK, которая пересекает стороны PR и PS и продолжение стороны RS. Имеем:
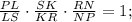
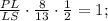
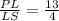
Внимание для тех, кто хочет (и знает, как) сделать сайт лучше и комфортнее! В данный момент я имею в виду не преодоление тех очевидных недостатков, которые становятся очевидными в первые пять минут, а плохую работу встроенного TEX'а. Впечатление, что здешние айтишники не знают, как решить возникающие проблемы. Предложите им свои услуги!
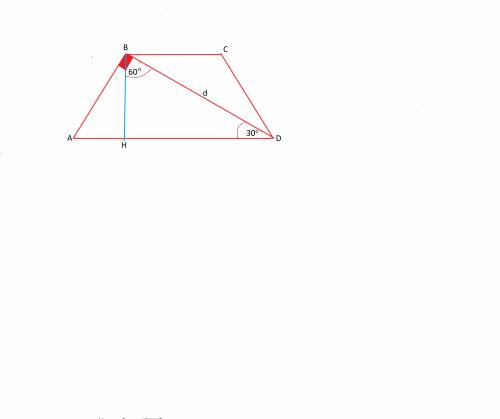
BH=√a^2-(a/2)^2=√3*a/2
Тогда площадь равна S=3a/2*√3*a/2 =3√3a^2/4