
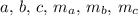 - длины сторон и медиан треугольника ABC,
- длины сторон и медиан треугольника ABC, 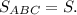 Воспользовавшись формулу
Воспользовавшись формулу 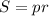 и то, что
и то, что 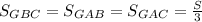 , получаем, что нужно доказать неравенство.
, получаем, что нужно доказать неравенство.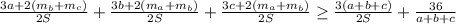
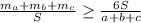
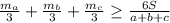
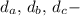 расстояния от точки G к сторонам a, b, c треугольника АВС. Очевидно, что
расстояния от точки G к сторонам a, b, c треугольника АВС. Очевидно, что 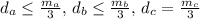 Также имеем
Также имеем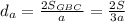 . Аналогично,
. Аналогично, 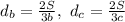
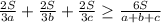 , которое равносильна неравенству, что выражает отношение между средним арифметическим и средним гармоническим 3 положительных чисел:
, которое равносильна неравенству, что выражает отношение между средним арифметическим и средним гармоническим 3 положительных чисел: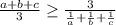
Определите, существует ли треугольник со сторонами:
5м.,8м. и 6м.
Поясните свой ответ. 2б.
Задача 3
В равнобедренном треугольнике BCE с основанием BE проведена биссектриса BK. Найдите
угол BKE , если уголE равен 40°.(чертеж обязателен) 5б.
Задача 4
В прямоугольнике ABCD проведена диагональ BD. Углы ,образованные этой диагональю равны угол ADB=15°,угол BDC=75°.
Докажите, что AD параллельно BC.(чертеж обязателен) 6б.
Задача 5
Любая точка перпендикуляра, проходящего через середину данного отрезка, равноудалена от его концов. ДОКАЖИТЕ ДАННОЕ УТВЕРЖДЕНИЕ