1) 68°, 68°, 44°.
2) 40°, 40°, 100°.
3) 110°, 35°, 35°.
4) 50°, 560°, 100°.
Объяснение
1) Внешний угол при основании равнобедренного треугольника равен 112°. Определите все углы треугольника.
Решение.
Внутренние углы при основании равны 180° - 112°=68°;
Угол при вершине равен 180°-2*68°=44°.
***
2) Внешний угол при основании равнобедренного треугольника равен 140°. Определите все углы треугольника.
Решение.
Внутренние углы при основании равны 180° - 140° = 40°.
Угол при вершине равен 180°-2*40°=100°.
***
3) Внешний угол при вершине равнобедренного треугольника равен 70°. Определите все углы треугольника.
Решение.
Внутренний угол при вершине равен 180° - 70°=110°.
На два угла при основании осталось (180° - 110°)/2=35°
***
4) В треугольнике АВС стороны АС и ВС равны. Внешний угол при вершине В равен 130°. Определите все углы треугольника.
Решение.
Внутренний угол при вершине равен 180° -130°=50°;
∠А = ∠В = 50°.
∠С=180° - 2 * 50°=80°.
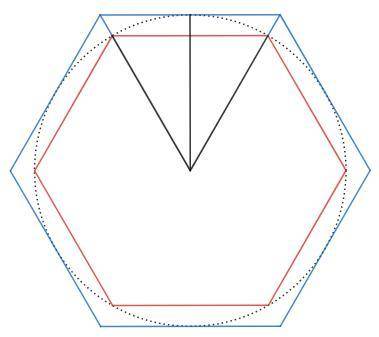
В окружность вписан правильный шестиугольник со стороной 3√3. Около окружности описан правильный шестиугольник, найдите сторону этого шестиугольника.
Рассмотрим вписанный шестиугольник (красный).
Проведем радиусы, угол между ними равен 1/6 полного угла, 60.
Равнобедренный треугольник с углом 60 - равносторонний.
Таким образом, радиус окружности равен стороне красного шестиугольника, 3√3.
Рассмотрим описанный шестиугольник (синий).
Соединим две вершины с центром - получим равносторонний треугольник.
Высота этого треугольника (h) - радиус вписанной окружности, 3√3.
(Радиус в точку касания перпендикулярен касательной.)
В равностороннем треугольнике
h/a =√3/2 => a =3√3 *2/√3 =6
лвовоыофшыотвлталааз