2
Объяснение:
L=3 длина хорды
S=6,25π площадь круга
Из формулы S=πR², найдем радиус круга.
R=√(S/π)=√(6,25π/π)=2,5 ед. радиус круга.
Найдем половину длины хорды.
L/2=3/2=1,5 ед. половина длины хорды
Половина длины хорды, радиус круга и расстояние от центра круга до хорды образуют прямоугольный треугольник, где радиус круга -это гипотенуза данного треугольника, а расстояние от центра до хорды и половина длины хорды - это катеты
По теореме Пифагора найдем второй катет.
√(R²-(L/2)²)=√(2,5²-1,5²)=√(6,25-2,25)=√4=2
ответ: расстояние от центра до хорды равно 2 ед.
ответ: ОТ=2√17см
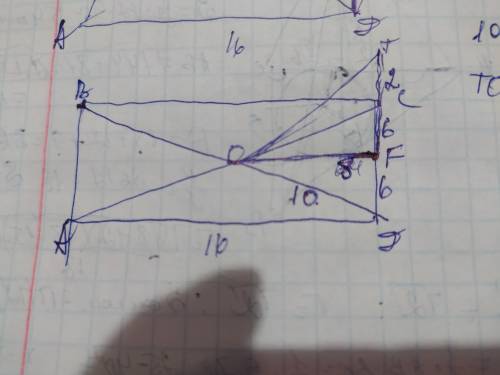
Объяснение: обозначим вершины прямоугольника ABCD с диагоналями АС и ВД, а точку их пересечения О. Одна диагональ прямоугольника делит его на 2 равных прямоугольных треугольника в которых стороны являются катетами а диагональ гипотенузой. Найдём диагональ прямоугольника по теореме Пифагора:
АС²=ВД²=АВ²+ВС²=12²+16²=256+144=400;
АС=ВД=√400=20см
Диагонали прямоугольника равны и пересекаясь делятся пополам поэтому АО=СО=ВО=ДО=20÷2=10см
СF=ДF=12÷2=6см
ОF является проекцией ТО на площадь прямоугольника. Рассмотрим полученный ∆ДОF. Он прямоугольный, ОF и ОД- катеты, а ОД- гипотенуза. Найдём OF по теореме Пифагора:
ОF²=ОД²-FД²=10²-6²=100-36=64;
ОF=√64=8см. Рассмотрим ∆OTF. Он также прямоугольный и ОF и ТF- катеты, а ОТ - гипотенуза. Найдём ОТ по теореме Пифагора: ОТ²=OF²+TF²=8²+2²=64+4=68;
OT=√68=2√17см
тогда один тупой угол равен x= (360 - 64)\2=148