В объяснении.
Объяснение:
1. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+3х+4х = 360° => х = 36°.
Больший угол равен 4х = 144°.
2. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+2х+4х = 360° => х = 40°.
Меньший угол равен 4х = 40°.
3. Площадь квадрата равна площади прямоугольника: 4*9 = 36 =>
Сторона квадрата равна √36 = 6 ед.
4. Площадь прямоугольника равна х*(х+2) = 24. Тогда
х² + 2х - 24 = 0. Решаем квадратное уравнение. => x = 6. (второй корень отрицательный)
Тогда большая сторона равна 6 + 2 = 8 ед.
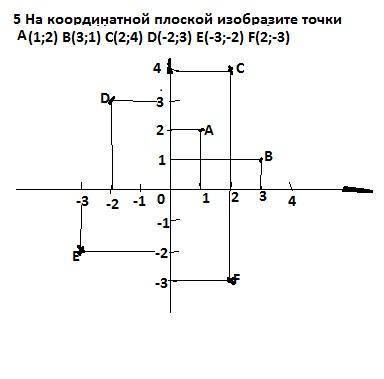
5. Смотри рисунок.
6. Уравнение окружности:
(Х - Хц)² + (Y-Yц)² = R² Тогда
а) Координаты центра: Ц(-5;2) Радиус = 4 ед.
б) Координаты центра: Ц(0;-3) Радиус = 3 ед.
BD^2 = AB^2 + AD^2, откуда BD = 13 см.
Б) проведём высоту CH к основанию AD. Тогда ABCH - прямоугольник, AH = BC и CH = AB = 5 см.
Треугольник CDH - прямоугольный с прямым углом CHD.
Причём так как угол D равен 45 градусам, то угол DCH = 45 градусов в силу того, что сумма острых углов прямоугольного треугольника равна 90 градусам.
Значит, треугольник CDH - равнобедренный. CH = DH = 5 см.
Ищем CD по теореме Пифагора:
CD^2 = CH^2 + DH^2, откуда CD = 5*sqrt(2) см. (Sqrt - это квадратный корень).
3) Треугольник ACH прямоугольный с прямым углом AHC.
AH = AD - DH = 12 - 5 = 7 см.
Ищем AC по теореме Пифагора:
AC^2 = AH^2 + CH^2, откуда AC = sqrt(74) см.