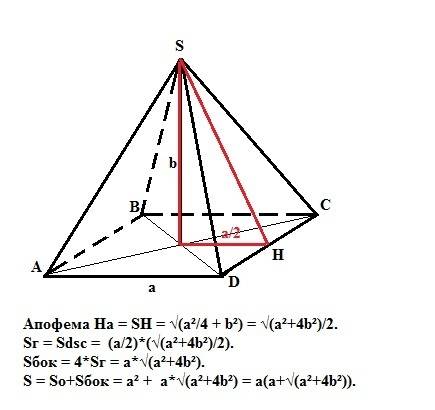
Пирамида правильная, значит в основании ее лежит квадрат, а вершина пирамиды проецируется в центр основания. Площадь полной поверхности пирамиды равна сумме площадей основания и боковой поверхности. Площадь основания нашей пирамиды равна So = a². Площадь боковой поверхности равна сумме четырех боковых граней пирамиды, каждая из которых равна Sг = (1/2)*а*На, где "а" - сторона основания, а "На" - апофема (высота) грани. Апофему грани найдем по Пифагору из прямоугольного треугольника, образованного высотой пирамиды, половиной стороны основания (катеты) и апофемой (гипотенуза). На = √(a²/4 + b²) = √(a²+4b²)/2.
Тогда площадь одной грани равна Sг = (a/2)*(√(a²+4b²)/2), площадь боковой поверхности пирамиды равна 4*Sг = а* √(a²+4b²).
Площадь полной поверхности пирамиды равна
S = a²+а* √(a²+4b²) = a(a+√(a²+4b²)).
б)4 Итак, что мы имеем: треугольник АВС, где угол А=90 градусов, и высота АD делит его на два прямоугольных треугольника.
Начнем с того, что попроще: треугольник ADB (угол D=90 градусов), катет AD=12, гипотенуза АВ=20, по теореме Пифагора 20^2=12^2+DB^2
Таким образом, сторона DB=16
Теперь рассмотрим второй треугольник, получившийся при делении большого треугольника высотой:
CDA, где угол D =90 градусов.
Катет AD=12, катет DC=X, гипотенуза AC=Y
По все той же теореме Пифагора получаем:
Y^2=12^2+X^2
Теперь рассмотрим исходный треугольник АВС
Катет АВ=20, катет АС=Y (смотри выше), гипотенуза СВ=X+16
По теореме Пифагора получаем:
20^2+Y^2=(X+16)^2 => Y^2=X^2+32X+256-400 => Y^2=X^2+32X-144
подставляем в уравнение Y^2=12^2+X^2 выраженное значение Y, получаем:
X^2+32X-144=12^2+X^2
32X=288
X=9
Таким образом, гипотенуза ВС=16+9=25
Катет АС=15
Косинус угла С равен отношению прилежащего катета к гипотенузе, т.е. cos C= AC/CB=15/25=3/5
Длина основания 4,21
А длина боковой стороны 9,01
Объяснение:
Длина боковой стороны 9,01 потому что
9,01-9,01<4,21<9,01+9,01